Kurt NÝrmark
Department of Computer Science, Aalborg University, Denmark
| Abstract Previous lecture Next lecture Index References Contents | In this lecture we will study the impact of the order of evaluation. |
| Referential transparency |
| Referential transparency Slide Annotated slide Contents Index References Textbook |
|
|
|
|
| An illustration of referential transparency Slide Annotated slide Contents Index References Textbook |
|
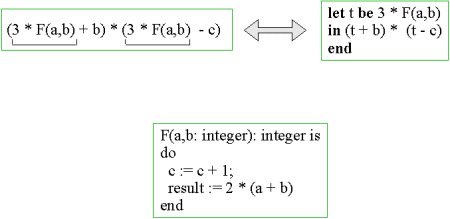
| Figure. It is possible to rewrite one of the expressions above to the other, provided that F is a function. Below, we have illustrated an example where F is of procedural nature. Notice that F assigns the variable c, such that it becomes critical to know how many times F is called. |  |
| Introduction to evaluation order |
| Arbitrary evaluation order - with some limits Slide Annotated slide Contents Index References Textbook |
|
| Figure. An illustration of an expression with subexpressions. |  |
|
| A motivating example Slide Annotated slide Contents Index References Textbook |
|
| Program: A constant function with an actual parameter expression, the evaluation of which never terminates.
|
|
| Program: A more concrete version of the expression from above. The function infinite-calculation just calls itself without ever terminating. |
|
| A motivating example - clarification Slide Annotated slide Contents Index References Textbook |
|
| Program: A constant function with an actual parameter expression, the evaluation of which never terminates.
|
|
| Program: A variation of the example in Scheme. |
|
|
| Rewrite rules, reduction, and normal forms |
| Rewrite rules Slide Annotated slide Contents Index References Textbook |
|
|
| The alpha rewrite rule Slide Annotated slide Contents Index References Textbook |
|
| The concept alpha conversion: Formal parameters of a lambda expression can be substituted by other names, which are not used as free names in the body |
| Legal conversion: |
| Table. An example of an alpha rewriting. The name a replaces x and the name b replaces y. |
|
| Illegal conversion: |
| Table. Examples of an illegal alpha conversion. f is a free name in the lambda expression. A free name is used, but not defined (bound) in the lambda expression. In case we rename one of the parameters to f, the free name will be bound, hereby causing an erroneous name binding. |
|
|
| The beta rewrite rule Slide Annotated slide Contents Index References Textbook |
|
| The concept beta conversion: An application of a function can be substituted by the function body, in which formal parameters are substituted by the corresponding actual parameters |
| Legal conversions: |
| Table. Examples of beta conversions. In all the three examples the function calls are replaced by the bodies. In the bodies, the formal parameters are replaced by actual parameters. |
|
|
| The eta rewrite rule Slide Annotated slide Contents Index References Textbook |
|
| The concept eta conversion: A function f, which only passes its parameters on to another function e, can be substituted by e |
| (lambda(x) (e x)) <=> e provided that x is not free in the expression e |
| Legal conversion: |
| Table. An example of an eta rewriting. |
|
| Illegal conversion: |
| Table. An example of an illegal eta conversion. The eta conversion rule says in general how 'e' is lifted out of the lambda expressions. In this example, e corresponds to the emphasized inner lambda expression (which is blue on a color medium.) However, x is a free name in the inner lambda expression, and therefore the application of the eta rewrite rule is illegal. |
|
|
| Normal forms Slide Annotated slide Contents Index References Textbook |
|
| The concept normal form: An expressions is on normal form if it cannot be reduced further by use of beta and eta conversions |
|
|
|
| The ordering of reductions Slide Annotated slide Contents Index References Textbook |
|
| The concept normal-order reduction: Using normal-order reduction, the first reduction to perform is the one at the outer level of the expression | ||
| The concept applicative-order reduction: Using applicative-order reduction, the first reduction to perform is the inner leftmost reduction |
|
| An example of normal versus applicative evaluation Slide Annotated slide Contents Index References Textbook |
|
| Figure. Normal vs. applicative reduction of a Scheme expression | 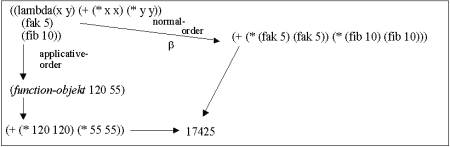 |
| Program: The necessary Scheme stuff to evaluate the expression. |
|
|
| Theoretical results Slide Annotated slide Contents Index References Textbook |
|
| Figure. The rewriting => is confluent if for all e, e1 and e2, for which e => e1 and e => e2, there exists an e3 such that e1 => e3 and e2 => e3 | 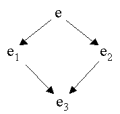 |
| The first Church-Rosser theorem. Rewriting with beta and eta conversions are confluent. |
| The second Church-Rosser theorem. If e0 => ... => e1, and if e1 is on normal form,
then there exists a normal order reduction of e0 to e1 |
|
| Practical implications Slide Annotated slide Contents Index References Textbook |
|
|
|
| Conditionals and sequential boolean operators Slide Annotated slide Contents Index References Textbook |
|
|
|
| Lazy evaluation Slide Annotated slide Contents Index References Textbook |
|
| The concept lazy evaluation: Lazy evaluation is an implementation of normal-order reduction which avoids repeated calculation of subexpressions |
| Figure. An illustration of lazy evaluation of a Scheme expression. Notice, that Scheme does not evaluate the expression in this way. Scheme uses applicative-order reduction. |  |
|
| Delayed evaluation and infinite lists in Scheme |
| Delayed evaluation in Scheme Slide Annotated slide Contents Index References Textbook |
|
| Syntax: |
|
| Syntax: |
|
| Program: A principled implementation of delay and force in Scheme. |
| Program: Real implementations of delay. The first definition uses the R5RS macro facility,
whereas the last one uses a more primitive macro facility, which happens to be supported in MzScheme. |
|
| Examples of delayed evaluation Slide Annotated slide Contents Index References Textbook |
| Table. Examples of use of delay and force. |
|
| Infinite lists in Scheme: Streams Slide Annotated slide Contents Index References Textbook |
|
| Program: Stream primitives. Notice the way head is defined to be an alias of car. |
| Program: An implementation of cons-stream in R5RS Scheme. |
|
|
| Example streams Slide Annotated slide Contents Index References Textbook |
| Table. Examples of streams. ones is an infinite streams of the element 1. stream-section is a function that returns a finite section of a potentially infinite stream. nat-nums is stream of all the natural numbers, made by use of the recursive function integers-starting-from. The fourth row shows an alternative definition of nat-nums. Finally, fibs is the infinite stream of Fibonacci numbers. |
|
| Program: The functions stream-section and add-streams. |
| Program: All Scheme stream stuff collected in one file. |
| Stream example: The sieve of Eratosthenes Slide Annotated slide Contents Index References Textbook |
|
| Program: The sieve stream function. |
|
| Figure. An illustration of the generation of prime numbers in The Sieve of Eratosthenes | 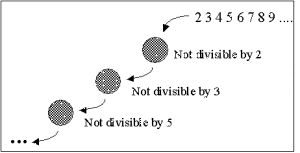 |
| Applications of The sieve of Eratosthenes Slide Annotated slide Contents Index References Textbook |
|
| Table. The first 25 prime numbers made by sieving a sufficiently long prefix of the integers starting from 2. |
|
| Program: All the functions necessary to use the Sieve of Eratosthenes. In addition, however, you must load the Scheme stream stuff.
The most remarkable function is filter-streams, which illustrates that
it is necessary to rewrite all our classical higher order function to
stream variants. This is clearly a drawback! |
|
Chapter 5: The Order of Evaluation
Course home Author home About producing this web Previous lecture (top) Next lecture (top) Previous lecture (bund) Next lecture (bund)
Generated: January 3, 2014, 09:34:07