


   | The Order of Evaluation |
At this point in the material it will be assumed that the reader is motivated to study evaluation order in some detail.
An evaluation of an expression can be understood as a transformation of the expressions which preserves its meaning. In this chapter we will see that transformations can be done incrementally in rewriting steps. A rewriting of an expression gives a new expression which is semantically equivalent to the original one. Usually, we go for rewritings which simplify an expression. In theory, however, we could also rewrite an expression to more complicated expression.
In this chapter we will formally characterize the value of an expression, using the concept of a normal form. We will see that the value of an expression is an expression in itself that cannot be rewritten to simpler forms by use of any rewriting rules.
As a key insight in this chapter, we will also see that an expression can be reduced to a value (a normal form) in many different ways. We will identify and name a couple of these, and we will discuss which of the evaluation strategies is the 'best'.
20.1. Rewrite rules
Contents Up Previous Next Slide Subject index Program index Exercise index
This section gives an overview of the rewrite rules, we will study in the subsequent sections.
The rewrite rules define semantics preserving transformations of expressions The goal of applying the rewrite rules is normally to reduce an expression to the simplest possible form, called a normal form. |
|
The Beta conversion corresponds to the substitution model of function calls, which is explained in [Abelson96]. (See section of 1.1.5 of [Abelson96] for the details).
20.2. The alpha rewrite rule
Contents Up Previous Next Slide Subject index Program index Exercise index
The first rewrite rule we encounter is called the alpha rewrite rule. From a practical point of view this rule is not very interesting, however. The rule tells under which circumstances it is possible to use other names of the formal parameters. Recall in this context that the formal parameter names are binding name occurrences, cf. Section 8.8.
An alpha conversion changes the names of lambda expression formal parameters |
Here comes the formulation of the alpha rewrite rule.
|
Recall in the context of this discussion that a free name in a construct is applied, but not bound (or defined) in the construct. See Section 8.11 for additional details about free names.
In Table 20.1 we see an example of a legal use of the alpha rewrite rule. The formal names x and y of the lambda expression are changed to a and b, respectively. It is fairly obvious that this causes no problems nor harm. The resulting lambda expression is fully equivalent with the original one.
| Expression | Converted Expression |
(lambda (x y) (f x y)) | (lambda (a b) (f a b)) |
| Table 20.1 An example of an alpha rewriting. The name a replaces x and the name b replaces y. |
More interesting, we show an example of an illegal use of the alpha rewrite rule in Table 20.2. Again we change the name x to a. The name of the other formal parameter is changed to f. But f is a free name in the lambda expression. It is easy to see that the converted expression in Table 20.2 has changed its meaning. The name f is now bound in the formal parameter list. Thus, the rewriting in Table 20.2 is illegal.
| Expression | Converted Expression |
(lambda (x y) (f x y)) | (lambda (a f) (f a f)) |
| Table 20.2 Examples of an illegal alpha conversion. f is a free name in the lambda expression. A free name is used, but not defined (bound) in the lambda expression. In case we rename one of the parameters to f, the free name will be bound, hereby causing an erroneous name binding. |
20.3. The beta rewrite rule
Contents Up Previous Next Slide Subject index Program index Exercise index
The beta rewrite rule is the one to watch carefully, due to its central role in any evaluation process that involves the calling of functions.
A beta conversion tells how to evaluate a function call |
The beta rewrite rules goes as follows.
|
It is worth noticing that there are no special conditions for the application of the beta rewrite rule. In that way the rule is different from both the alpha rewrite rule, which we studied in Section 20.2, and it is also different from the eta rewrite rule which we encounter in Section 20.4 below. All the examples in Table 20.3 are legal examples of beta rewritings.
| Expression | Converted Expression |
((lambda(x) (f x)) a) | (f a) |
((lambda(x y) (* x (+ x y))) (+ 3 4) 5) | (* 7 (+ 7 5)) |
((lambda(x y) (* x (+ x y))) (+ 3 4) 5) | (* (+ 3 4) (+ (+ 3 4) 5)) |
| Table 20.3 Examples of beta conversions. In all the three examples the function calls are replaced by the bodies. In the bodies, the formal parameters are replaced by actual parameters. |
Be sure to understand that the beta rewrite rule tells us how to implement a function call, at least in a principled way. In a practical implementation, however, the substitution of formal parameters by (more or less evaluated) actual parameters is not efficient. Therefore, in reality, the bindings of the formal parameters are organized in name binding frames, in so-called environments. Thus, instead of name substitution (as called for in the beta rewrite rules), the formal names are looked up in a name binding environment, when they are needed in the body of the lambda expression.
The implementation of eval in a Scheme interpreter describes the details of a practical and real life use of the beta rewrite rule. See Section 25.3 for additional details.
20.4. The eta rewrite rule
Contents Up Previous Next Slide Subject index Program index Exercise index
The eta rewrite rules transforms certain lambda expressions. As such the eta rewrite rule is similar to the alpha rewrite rule, but radically different from the beta rewrite rule.
An eta conversion lifts certain function calls out of a lambda convolute |
In loose terms, the eta rewrite rule can be formulated in the following way. Be aware, however, that there is a condition associated with applications of the eta rewrite rule. The condition is described below.
|
Here is a slightly more formal - and more precise - description of the eta rewrite rule:
In the same way as above for alpha conversions in Section 20.2 we will give examples of legal and illegal uses of the eta rule.
The example in Table 20.4 shows that the lambda expression around square is superfluous. In the eta-rewritten expression, the lambda surround of square is simply discarded.
| Expression | Converted Expression |
(lambda (x) (square x)) | square |
| Table 20.4 An example of an eta rewriting. |
It is slightly more complicated to illustrate an illegal use of the rule. In the expression of the left cell in Table 20.5 we are attempting to eliminate the outer lambda expression by use of the eta rewrite rule. Notice, however, that x is free in the inner blue lambda expression. Therefore the eta rewriting illustrated in Table 20.5 is not legal. By applying the rewriting rule on the left part of Table 20.5 anyway we loose the binding of x, and therefore the rewriting does not preserve the semantics of the left cell expression.
| Expression | Converted Expression |
(lambda(x) ((lambda(y) (f x y)) x)) | (lambda(y) (f x y)) |
| Table 20.5 An example of an illegal eta conversion. The eta conversion rule says in general how 'e' is lifted out of the lambda expressions. In this example, e corresponds to the emphasized inner lambda expression (which is blue on a color medium.) However, x is a free name in the inner lambda expression, and therefore the application of the eta rewrite rule is illegal. |
This completes our discussion of rewriting rules, and we will now look at the concept of normal forms.
20.5. Normal forms
Contents Up Previous Next Slide Subject index Program index Exercise index
As already mentioned above, the value v of an expression e is a particular simple expression which is semantically equivalent with e. The expression v is obtained from e by a number of rewriting steps.
Normal forms represent our intuition of the value of an expression |
Here is the definition of a normal form.
|
Notice in the definition that we talk about reduction. By this is meant application of the rewrite rules 'from left to right'.
|
Normal forms are simple to understand. But there are a number of interesting and important questions that need to be addressed. One of them is formulated below.
Is a normal form always unique? |
The answer to the question will be found in Section 20.9.
20.6. The ordering of reductions
Contents Up Previous Next Slide Subject index Program index Exercise index
As discussed in Section 19.3 we can expect that the concrete order of evaluation steps will matter, especially in the cases where errors or infinite calculations are around in some of the subexpressions.
Evaluation steps are now understood as reductions with the beta or eta rewrite rule.
In this section we will identify and name a couple of evaluation strategies or plans. Such a strategy determines the order of use of the beta and eta reduction rules.
Given a complex expression, there are many different orderings of the applicable reductions |
|
|
Let it be clear here, that many other evaluation strategies could be imagined. The practical relevance of additional strategies is another story, however.
Applicative-order reduction represents 'the usual' evaluation strategy, used for expressions in most programming languages. Normal-order reduction represents a new approach, which is used in a few contemporary functional programming languages.
In Section 20.10 we will discuss examples of the special forms mentioned in the item discussing the applicative-order reduction.
20.7. An example of normal versus applicative evaluation
Contents Up Previous Next Slide Subject index Program index Exercise index
Let us illustrate the difference between normal-order reduction and applicative-order reduction via a concrete example.
Reduction of the expression ((lambda(x y) (+ (* x x) (* y y))) (fak 5) (fib 10)) |
The example involves an application of the blue function (lambda(x y) (+ (* x x) (* y y))) on the actual parameters (fak 5) and (fib 10). The functions fak and fib are shown in Program 20.1 .
In Program 20.1 we show definitions of fak and fib, together with the example expression.
1 2 3 4 5 6 7 8 9 | (define (fak n)
(if (= n 0) 1 (* n (fak (- n 1)))))
(define (fib n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 1)) (fib (- n 2))))))
((lambda(x y) (+ (* x x) (* y y))) (fak 5) (fib 10)) | |||
|
In Figure 20.1 applicative-order reduction is outlined in the leftmost path of the graph. With applicative-order reduction we first evaluate the lambda expression, then (fak 5) and (fib 10). The evaluation of the lambda expression gives a function object. Notice that the expensive calculations of (fak 5) and (fib 10) are only made once. The last step before the addition and the multiplications is a beta reduction, with which the function is called.
The normal order reduction is illustrated with the path to the right in Figure 20.1. The outer reduction is a beta reduction, in which we substitute the non-reduced parameter expressions (fak 5) and (fib 10). Notice that the calculation of (fak 5) and (fib 10) are made twice.
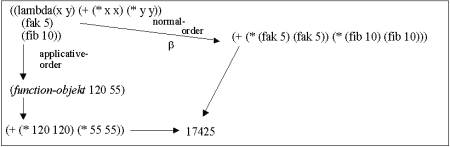
| Figure 20.1 Normal vs. applicative reduction of a Scheme expression |
As an immediate insight from the example we will emphasize the following:
It appears to be the case that normal order reduction can lead to repeated evaluation of the same subexpression |
20.8. Theoretical results
Contents Up Previous Next Slide Subject index Program index Exercise index
We will now cite some theoretical results of great importance to the field.
The theoretical results mentioned on this page assure some very satisfactory properties of functional programming |
The results are based on a definition of confluence, which appears in the figure below.
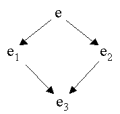
| Figure 20.2 The rewriting => is confluent if for all e, e1 and e2, for which e => e1 and e => e2, there exists an e3 such that e1 => e3 and e2 => e3 |
The results which we will use below are the following:
The practical consequences of the results will be discussed in the following section.
20.9. Practical implications
Contents Up Previous Next Slide Subject index Program index Exercise index
We will here describe the practical consequences of the theoretical results mentioned on the previous page |
|
Because rewriting with beta and eta reduction is confluent, according to the first Church-Rosser theorem in Section 20.8, we see that there can be no dead ends in an evaluation process. Assume there is, and you will get an immediate contradiction.
The middle item is of particular importance because it guaranties that a normal form is unique. Assume that two different normal forms exist, and get a contraction with the first of the theorems.
The last result is a direct consequence of the second Church-Rosser theorem. It says more or less that normal-order reduction is the most powerful evaluation strategy. Notice, however, the efficiency penalties with are involved, due to repeated evaluation of expressions. This is the theme of Section 20.11.
We can summarize as follows.
Normal-order reduction is more powerful than the applicative-order reduction Scheme and ML uses applicative-order reduction Haskell is an example of a functional programming language with normal-order reduction |
20.10. Conditionals and sequential boolean operators
Contents Up Previous Next Slide Subject index Program index Exercise index
In languages with applicative-order reduction there is a need to control the evaluation process in order to avoid the traps of erroneous and infinite calculations. In this section we review a couple of widely used and important forms from Scheme and Lisp. The evaluation control of these should in particular be noticed.
There are functional language constructs - special forms - for which applicative order reduction would not make sense |
|
|
In the items above we discuss the general semantics of if and and. In the deepest items we give a concrete examples of if and and where the evaluation order matters.
20.11. Lazy evaluation
Contents Up Previous Next Slide Subject index Program index Exercise index
Lazy evaluation is a particular implementation of normal-order reduction which takes care of the lurking multiple evaluations identified in Section 20.7.
We will now deal with a practical variant of normal-order reduction |
|
In Figure 20.3 we show an evaluation idea which is based on normal-order reduction without multiple evaluation of parameters, which are used two or more times in the body of a function.
It is not our intention in this material to go deeper into the realization of an interpreter that supports lazy evaluation.

| Figure 20.3 An illustration of lazy evaluation of a Scheme expression. Notice, that Scheme does not evaluate the expression in this way. Scheme uses applicative-order reduction. |
This end the general coverage of evaluation order. In the next chapter we will see how to explore the insights from this chapter in Scheme, which is a language with traditional, applicative-order reduction.
20.12. References
| [Abelson96] | Abelson, H., Sussman G.J. and Sussman J., Structure and Interpretation of Computer Programs, second edition. The MIT Press, 1996. |