


   | Higher-order Functions |
In this chapter we will focus on higher-order functions that work on lists. It turns out that the appropriate combinations of these make it possible to solve a variety of different list processing problems.
| 15.1 Classical higher-order functions: Overview | 15.5 Filtering |
| 15.2 Mapping | 15.6 The filtering function |
| 15.3 The mapping function | 15.7 Examples of filtering |
| 15.4 Examples of mapping |
15.1. Classical higher-order functions: Overview
Contents Up Previous Next Slide Subject index Program index Exercise index
There exists a few higher-order functions via which a wide variety of problems can be solved by simple combinations |
|
The functions mentioned above represent abstractions of algorithmic patterns in the
functional paradigm |
15.2. Mapping
Contents Up Previous Next Slide Subject index Program index Exercise index
A mapping function applies a function on each element of a list and returns the list of these applications The function map is an essential Scheme function |
The idea of mapping is illustrated below.
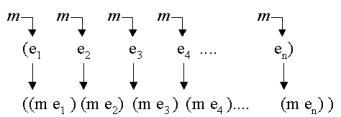
| Figure 15.1 Mapping a function m on a list. m is applied on every element, and the list of these applications is returned. |
15.3. The mapping function
Contents Up Previous Next Slide Subject index Program index Exercise index
1 2 3 4 5 | (define (mymap f lst)
(if (null? lst)
'()
(cons (f (car lst))
(mymap f (cdr lst))))) | |||
|
In contrast to the function mymap on this page , write an iterative mapping function which is tail recursive.
Test your function against mymap on this page, and against the native map function of your Scheme system.
SolutionIn an earlier section we have shown the application of some very useful table manipulation functions. Now it is time to program these functions, and to study them in further details.
Program the functions transpose, eliminate-row, and eliminate-column, as they have been illustrated earlier. As one of the success criteria of this exercise, you should attempt to use higher-order functions as much and well as possible in your solutions.
Hint: Program a higher-order function, (eliminate-element n). The function should return a function which eliminates element number n from a list.
There is no solution to this exercise
15.4. Examples of mapping
Contents Up Previous Next Slide Subject index Program index Exercise index
| Expresion | Value |
(map string? (list 1 'en "en" 2 'to "to")) | (#f #f #t #f #f #t) |
(map (lambda (x) (* 2 x)) (list 10 20 30 40)) | (20 40 60 80) |
(ul
(map
(compose li
(compose b
(lambda (x)
(font-color red x))))
(list "a" "b" "c")
)
) |
|
| Same as above | <ul>
<li>
<b><font color = "#ff0000">a</font></b>
</li>
<li>
<b><font color = "#ff0000">b</font></b>
</li>
<li>
<b><font color = "#ff0000">c</font></b>
</li>
</ul> |
| Table 15.1 In the first row we map the string? predicate on a list of atoms (number, symbols, and strings). This reveals (in terms of boolean values) which of the elements that are strings. In the second row of the table, we map a 'multiply with 2' function on a list of numbers. The third row is more interesting. Here we map the composition of li , b , and red font coloring on the elements a, b, and c. When passed to the HTML mirror function ul , this makes an unordered list with red and bold items. Notice that the compose function used in the example is a higher-order function that can compose two or more functions. The function compose from lib/general.scm is such a function. Notice also that the HTML mirror function ul receives a list, not a string. The fifth and final row illustrates the raw HTML output, instead of the nicer rendering of the unordered list, which we used in the third row. |
15.5. Filtering
Contents Up Previous Next Slide Subject index Program index Exercise index
A filtering function applies a predicate (boolean function) on every element of a list.
Only elements on which the predicate returns true are returned from the filtering function. The function filter is not an essential Scheme function - but is part of the LAML general library |
The figure below illustrates the filtering idea.

| Figure 15.2 Filtering a list with a predicate f. The resulting list is the subset of the elements which satisfy f (the elements on which f returns true). |
15.6. The filtering function
Contents Up Previous Next Slide Subject index Program index Exercise index
For practical purposes it is important to have a memory efficient filter function |
As a consequence of the observation above, we now program a tail recursive version of filter. Notice that it is the function filter-help, which does the real filtering job.
1 2 3 4 5 6 7 8 9 | (define (filter pred lst)
(reverse (filter-help pred lst '())))
(define (filter-help pred lst res)
(cond ((null? lst) res)
((pred (car lst))
(filter-help pred (cdr lst) (cons (car lst) res)))
(else
(filter-help pred (cdr lst) res)))) | |||
|
The filter function illustrated in the material is memory efficient, using tail recursion.
Take a moment here to implement the straightforward recursive filtering function, which isn't tail recursive.
Solution
15.7. Examples of filtering
Contents Up Previous Next Slide Subject index Program index Exercise index
| Expression | Value |
(filter even? '(1 2 3 4 5)) | (2 4) |
(filter (negate even?) '(1 2 3 4 5)) | (1 3 5) |
(ol
(map li
(filter string?
(list
1 'a "First" "Second" 3)))) |
|
| Same as above | <ol> <li>First</li> <li>Second</li> </ol> |
| Table 15.2 In the first row we filter the first five natural numbers with the even? predicate. In the second row, we filter the same list of numbers with the odd? predicate. Rather than using the name odd? we form it by calculating (negate even?) . We have seen the higher-order function negate earlier in this lecture. The third and final example illustrates the filtering of a list of atoms with the string? predicate. Only strings pass the filter, and the resulting list of strings is rendered in an ordered list by means of the mirror function of the ol HTML element. |