The MDPDist Mathematica package

On-the-fly exact computation of bisimilarity distances for Markov Decision Process with rewards

Authors: Giorgio Bacci, Giovanni Bacci, Kim G. Larsen, and Radu Mardare

In this tutorial we present the main features of the MDPDist package. This Mathematica package implements an on-the-fly method for computing the bisimilarity pseudometric of Ferns et al. [1] for Markov Decision Process with rewards. The algorithm implemented in this package is an exension of the on-the-fly method recently proposed in [2] for Markov Chains.

Preliminaries

Markov Decision Processes and Bisimulation

A probability distribution over a nonempty enumerable set S is a function μ : S → [0,1] such that . We denote by Δ(S) the set of probability distributions over S.

Definition (Markov Decision Process). A Markov Decision Process with rewads (MDP) is a tuple M =(S,A,τ,ρ) consisting of a finite nonempty set S of states, a finite nonempty set A of actions, a transition function τ : S × S → Δ(S), and a reward function τ ∶ S × A → R.

The operational behavior of an MDP M =(S,A,τ,ρ) is as follows: the process in the state chooses nondeterministically an action a ∈ A and it changes the state to , with the probabilty τ(,a)(). The choice of the action a made in is rewarded by ρ(,a). The exectutions are transition sequences w = (,),(,),....; the challenge is to find strategies for choosing the actions in order to maximize the accumulated reward , where λ ∈ (0,1) is the discount factor. A strategy is given by a function π : S → Δ(A), called policy, where π()(a) is the probabilty distribution over executions defined, for arbitrary w = (,),(,)...., by . The value of s according to π is characterized by , where Ω(w) is the set of executions from s.

Definition (Stocastic Bisimulation). Let M =(S,A,τ,ρ) be an MDP. An equivalence relation R ⊆ S × S is a stocatic bisimulation if whenever (s,t) ∈ R then, for all a ∈ A, ρ(s,a) = ρ(t,a) and, for all R-equivalence classes C, . Two states s,t ∈ S are stocatic bisimilar, written s ∼ t, if they are related by some stochastic bisimulation on M.

Bisimilarity Pseudometric

To cope with the problem of measuring how similar two MDPs are, Ferns et al. [1] defined a bisimilarity pseudometric that measures the behavioral similarity of two non-bisimilar MDPs. This is defined as the least fixed point of a transformation operator on functions in S × S → [0,∞).
Consider an arbitrary MDP M =(S,A,τ,ρ) and a discount factor λ ∈ (0,1). The set S × S → [0,∞) of [0,∞)-valued maps on S × S equipped with the point-wise partial order defined by d ⊆ d’ ⇔ d(s,t) ≤ d’(s,t), for all s,t ∈ S.
We define a fixed point operator , for d : S × S → [0,∞) and s,t ∈ S as

Where denotes the optimal value of a Transportation Problem with marginals τ(s,a) and τ(t,a) and costs given by d

is monotonic, thus, by Tarski’s fixed point theorem, its admits a least fixed point. This fixed point is the bisimilarity pseudometric.

Definition (Bisimilarity psudometric). Let M =(S,A,τ,ρ) be an MDP and λ ∈ (0,1) be a discount factor, then the λ-discounted bisimilarity pseudometric for M, written , is the lest fixed point of .

The pseudometric enjoys the property that two states are at distance zero if and only if they are bisimilar.

Getting started

The package can be loaded by setting as current directory the directory of the MDPDist package, then using the commad << (Get) as follows

Encoding and manipulating Markov Decision Processes

Encoding an MDP

An MPD M =(S,A,τ,ρ) with and is represented as a term of the form MPD[tm,rw,act] where
- tm is an n × m × n probability matrix such that tm[[i,k,j]] = for all 1 ≤ i,j ≤ n and all 1 ≤ k ≤ m,
- rw is an n × m real-valued matrix such that rw[[i,k]]= for all 1 ≤ i ≤ n and all 1 ≤ k ≤ m, and
- act is a list of pairwise distinct strings such that act[[k]] represents the action for all 1 ≤ k ≤ m.
A state is implicitly represented by its index 1 ≤ i ≤ n.

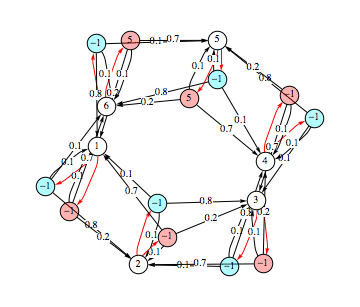
Assume we want to encode the following MDP M =(S,A,τ,ρ) with S = {1,2,3,4,5,6} and A = {inc, dec}, with the following intuitive operational behavior.  Given M in state i, the choice of the action inc causes the MDP to move in state i+1 with probability 0.8, and to stay in state i or to move in state i-1 both with probability 0.1. The choice of the action dec causes the MDP to move in state i-1 with probability 0.7, to stay in state i with probability 0.1, and to move in state i+1 with probability 0.2. The reward of choising an inc action is always -1, whereas the reward for a dec action is 5 if it is made from state 5 or 6, 0 otherwise.

Mathematica allows to easily define functions and lists, so that we can exploit these features in order to define the data structures that are needed to encode M

A represents the set of actions, τ is the transition function and ρ is the reward function.
One can obtain the respective transition and reward matrix using the built-in function Table as follows:

Then M is encoded by

Alternatively, one may use the functions MDPtm and MDPrw to construct the transition and the reward matrices listing only the values different from zero. Given the list of rules tmRules = { , the probabilty transition matrix induced by the probability transition function τ may be constructed by calling MDPtm[tmRules, n, m].
Analogously, for rwRules = { , one can construct the reward matrix induced by the reward function ρ by calling MDPrw[rwRules, n, m].

The list of rules may be given explicitly or using patterns. For example, the matrices tm and rw defined above can be constructed as follows

Manipulating MDPs

An MDP is dispayed by the function PlotMDP. States are represented as white nodes labeled with their respective index. Red edges exiting from each node represent a nondeterministic choice of an action. The chosen action is displayed as a colored node labeled with its associated reward, called choice node. Edges exiting form a choice node represent the probability distribution obtained after a nondeterministic choice. For example, the MDP mdp defined above is dispayed as follows

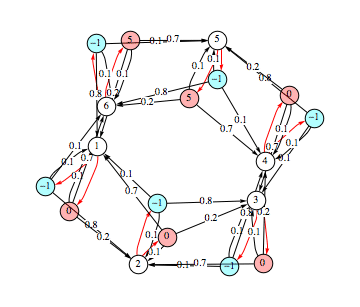
Given a sequence of MDPs, JoinMDP[] yields an MDP representing their disjoint union, where the indices representing the set of states are obtained shifting the indices of the states of its arguments according to their relative order in the sequence (e.g. if has n states, the index corresponding to the i-th state of in JoinMDP[,] is n + i).

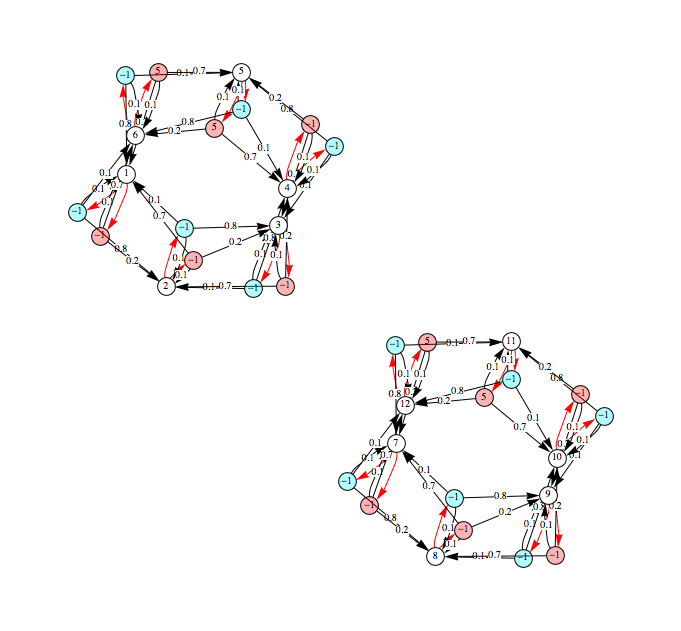
Computing Bisimilarity Distances

Given an MDP M, a discount factor λ, and a list of state pairs Q, BDistMDP[M,λ,Q] computes the distance associated with each pair of states (s,t) in Q. For example, taking MDP mdp considered so far, a discount factor 0.5 and a single-pair query Q = {(1,2)} we have

while for the query Q = {(1,2),(3,4),(6,5)} we have

If one is interested in computing the distance between all state pairs, it can use the alias All as follows

The computation can be traced setting the option Verbose to True. It will display the couplings encoutered during each iteration of the on-the-fly algorithm. This option can be also used to analyze how the algorithm explores the state space of the MDP.

One can provide some estimates in order to further reduce the exploration of the state space. This can be done using the option Estimates

Exact Computations

Mathematica allows one to perform exact computations over Rational numbers. Usually the Bellman-optimality equation system is computed approximately since it is in general a non-linear equation system. Despite this fact, our method is able to compute the exact result when the input MDP is rational-valued (i.e. both the transition fuction and the reward function are rational-valued)

For example, the MDP we considered so far can be rationalized as follows

now, the exact value of the distance can be computed setting the option Exact to True

(Asynchronous) Parallel Composition

Usually, MDPs are specified as the composition of several smaller sub-systems. To this end, several composition operators have been introduced, among them we recall the synchronous (and asynchronous) parallel composition or the probabilistic choice. This operators allows one to describe very large systems implicitly as the composition of more manageble sub-systems.

The BDistMDP function is able to directly handle MDPs defined as the (asyncronous) parallel composition of other systems. Having a sequence of MDPs , its (asyncronous) parallel composition can be implicity defined as a term CMDP[enc,{}] where enc represent the “encoding maps” that associates each composite state its ecoded state.
It is worth noting that CMDP[enc,{}] is treated as a term and CMDP is a simple data structure that does compute the parallel composition of  .

Let us consider a simple yet meaningful set of experiments performed on a collection of MDPs, parametric in the probabilities, modeling a pipeline. The following function specifies a an element of a pipeline with actions for i ∈ N. A pipeline is modeled as the parallel composition of different processing elements, that are connected in series by measn of synchronization on shared actions.

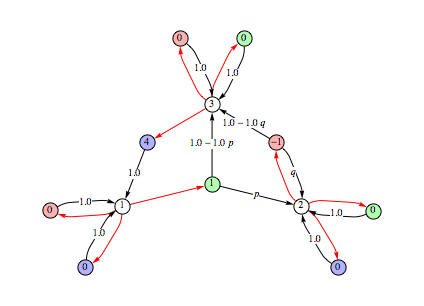
Let us define some element instances

The ecoding map associated with the composite system has to be computed using the function getEncodingMaps as follows

now the pipeline instance is encoded by the following term

The index of a state of the pipeline can be specified as a tuple of the form where is a state belonging to . The ecoding map defined above helps in retrieving the state index corresponding to the composite state. For example, the pair of state indices associated with the pair {{1,1,1},{1,2,1}} is given by

however, the function BDistMDP handles such composite pairs of states. For example, assuming λ= 1/2, the distance between the composite state {1,1,1} and {1,2,1} in  is

Bisimilarity Classes & Quotient

Due to the fact that (s,t) equals zero if and only if the states s and t are bisimilar, we can use the algorithm for computing in order to compute the bisimilarity classes and the bisimilarity quotient for an MDP.

The function BisimClassesMDP[M] returns the set of bisimilarity classes of M, that is S/∼.

The function BisimQuotientMDP[M] yields an MDP representing the bisimilarity quotient of M.

Created with Wolfram Mathematica 9.0