Kurt NÝrmark
Department of Computer Science, Aalborg University, Denmark
| Abstract Previous lecture Next lecture Index References Contents | In this side track lecture we will introduce the LAML system, which allows us to do web programming Scheme and in the functional programming paradigm |
| Closures revisited |
| Functions and closures Slide Annotated slide Contents Index References | On this page we review some of the properties of function object - also known as closures. The contents of this pages is taken directly from an earlier pages in this material. |
| The concept function object: A function object represents a function at run time. A function object is created as the value of a lambda expression | A function object is a first class value at run time, in the same way as numbers, lists and other data are values. This is different from more traditional programming languages, where procedural and functional abstractions have another status than ordinary data. | |
| The concept closure: A function object is also known as a closure. | The name 'closure' is related to the interpretation of free names in the body expression of the function. Free names are used, but not defined in the body. In a function object (or closure) the free names are bound in the context of the lambda expression. This is a contrast to the case where the free names are bound in the context of the application of the function. |
|
|
| Classes and objects in Scheme |
| Functions with private context Slide Annotated slide Contents Index References Textbook |
|
| Program: A template of a function with private context. The lambda expression appears in the context of the let name binding construct.
When the definition is evaluated a name binding context is established around
the lambda expression. The lambda expression is the only place in the program
which have a possibility to reach the name bindings. Therefore the name bindings
are local to the lambda expression.
The CONTEXT is a list of name bindings, as such name bindings appear in a let construct.
|
|
| Table. An example in which we abstract a (html (head (title..)) (body ...)) expression in a lambda expression, of which we define a private context. The context redefines the html and body functions to 'specialized' versions, with certain attributes. Notice the importance of the 'simultaneous name bindings' of let in the example (as explained in an earlier lecture). Also notice that we have discussed the modify-element higher-order function before. |
|
|
| Classes and objects Slide Annotated slide Contents Index References Textbook |
|
| Program: The send method which is used in the Point class. The function apply calls a function
on a list of parameters. This should be seen in contrast to a normal call, in which the individual parameters
are passed. |
|
| Program: The definition of a 'class Point ' with methods getx , gety , add , and type-of . On this page we have also defined the syntactical convenience function send that sends a message to an object. In MzScheme, be sure that you define send before Point (such that send in the add method refers to our send , and not an already existing and unrelated definition of
the name send ). |
|
| Program: All necessary stuff to play with Point. |
| Exercise 8.2. Points and Rectangle | The purpose of this exercise is to strengthen your understanding of functions used as classes in Scheme. First, play with the existing Point class defined on this page available from the on-line version of this material. As an example, construct two points and add them together. Also, construct two lists of each four points, and add them together pair by pair. Define a new method in the Point class called (move dx dy) , which displaces a point with dx units in the x direction and dy units in the y direction. We encourage you to make a functional solution in which move creates a new displaced point. After that you can make an imperative solution in which the state of the receiving point is changed. Finally, define a new class, Rectangle , which aggregates two points to a representation of a rectangle. Define move and area methods in the new class. As a practical remark to the 'class Point ' and the send primitive, be sure to define send before you define Point . (This is done to redefine an existing send procedure in MzScheme). |
| A general pattern of classes Slide Annotated slide Contents Index References Textbook |
|
| Program: A general template of a simulated class. construction-parameters are typically transferred to the let construct, which we want to play the role as
instance variables. Next comes explicitly defined methods, and last is the object handle called self .
Notice that the value returned by the class is the value of self - the object handle. |
|
| Program: Accompanying functions for instantiation and message passing. |
|
|
| Example of the general class pattern Slide Annotated slide Contents Index References Textbook |
|
| Program: The class Point implemented with use of the general class template. The Point class corresponds to the Point class defined on an earlier page.
Notice that the bindings of x and y in the let construct is superfluous in the example.
But due to the simultaneous name binding used in let constructs, they make sense.
Admittedly, however, the let construct looks a little strange.
|
|
| Program: All necessary stuff to play with Point. |
| Program: A sample construction and dialogue with point. |
|
| A general pattern of classes with inheritance Slide Annotated slide Contents Index References Textbook |
|
| Program: A general template of a simulated class with inheritance. |
|
| Program: A simulation of the root of a class hierarchy. |
|
| Program: Accompanying functions for instantiation, message passing, and method lookup. |
|
| An example of classes with inheritance Slide Annotated slide Contents Index References Textbook |
|
| Program: A specialization of Point which is called ColorPoint. |
|
| Program: All necessary stuff to play with ColorPoint. |
| Program: A sample construction and sample dialogue with ColorPoint. |
|
| Exercise 8.3. Color Point Extension | On this page we have introduced the class ColorPoint, which inherits from Color . In the sample dialogue with a couple of color points we have identified the problem that the sum of two color points is not a color point. Why is it so? You are now supposed to make a few changes in the classes Point and ColorPoint. In order to make it realistic for you to play with the classes, your starting point is supposed to be a pre-existing file, with all the useful stuff (available from the on-line version of this material). When you experiment with points and color-points, use M-x run-laml-interactively from Emacs.
|
| The interpretation of self Slide Annotated slide Contents Index References Textbook |
|
| Figure. Two different interpretations of self . We see two linear class hierarchies. The class C inherits from B, which in turn inherits from A. And similarly, F inherits from E, which inherits from D. The one to the left - in the green class hierarchy - is the naive one we have obtained in our templates and examples until now. The one to the right - in the yellow class hierarchy, shows another interpretation of self . Following this interpretation, self at all levels refer to the most specialized object part. | 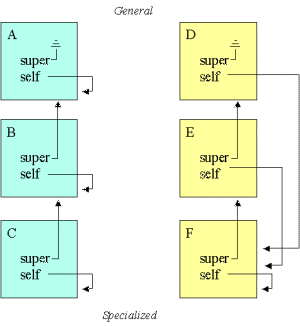 |
| A demo of virtual methods Slide Annotated slide Contents Index References Textbook |
|
| Program: A base class x . The method res sends the message get-state to itself. If an x object receives the message res , it will return the number 1. |
|
| Program: A class y that inherits from x . The y class redefines the method get-state . The y class inherits the method res .
If a y method receives the message res , it will be propagate to the x part of the object.
Due to the use of virtual methods, self in the x part refers to the y part. Therefore
the get-state message returns the y-state of the y part, namely 2. |
|
| Program: A dialogue using class x and class y. Instances of the classes x and y are created and res messages are send to both of them. |
|
| Program: The functions new-instance and virtual-operations. |
| Program: All the stuff necessary to play with x and y. The crucial observation is that the y object bound to the variable b returns the number 2 when we send it the res message. |
| Exercise 8.4. Representing HTML with objects in Scheme | This is an open exercise - maybe the start of a minor project. In the original mirror of HTML in Scheme, the HTML mirror functions, return strings. In the current version, the mirror functions return an internal syntax tree representation of the web documents. With this, it is realistic to validate a document against a grammar while it is constructed. In this exercise we will experiment with an object representation of a web document. We will use the class and object representation which we have introduced in this lecture. Construct a general class html-element which implement the general properties of a HTML element object. These include:
In addition, construct one or more examples of specific subclasses of html-element , such as html , head , or body. These subclasses should have methods to access particular, required constituents of an element instance, such as the head and the body of a HTML element, and title of a head element. Also, the concrete validation predicate must be redefined for each specific element. |
| Collected references Contents Index |
|
Chapter 8: Object-oriented programming in Scheme
Course home Author home About producing this web Previous lecture (top) Next lecture (top) Previous lecture (bund) Next lecture (bund)
Generated: January 3, 2014, 09:49:30