Kurt Nørmark
Department of Computer Science, Aalborg University, Denmark

Abstract Previous lecture Next lecture Index References Contents

In this lecture we will explore the higher-order functions, both on classical ground and with examples from the WWW domain.

"NEXT: Factorial. Recursive variant"

(define (fak0 n)
  (if (= n 0)
      1
      (* n (fak0 (- n 1)))))

(fak0 10)

"NEXT: Factorial. Iterative variant"

(define (fak1 n r)
  (if (= n 0)
      r
      (fak1 (- n 1) (* r n))))

(fak1 10 1)

"NEXT: Number intervals. Recursive variant"

(define (number-interval f t)
 (if (<= f t)
     (cons f (number-interval (+ f 1) t))
    '()))

(number-interval 1 10)
(number-interval 10 1)

"NEXT: Number intervals. Iterative variant"

(define (number-interval-iter f t)
  (reverse (number-interval-iter-help f t '())))


(define (number-interval-iter-help f t res)
  (if (<= f t)
      (number-interval-iter-help (+ f 1) t (cons f res))
      res))

(number-interval-iter 1 10)
(number-interval-iter 10 1)

"NEXT: String-merge. Recursive variant"

(define (string-merge str-list-1 str-list-2)
 (cond ((null? str-list-1) (apply string-append str-list-2))
       ((null? str-list-2) (apply string-append str-list-1))
       (else (string-append
              (car str-list-1) (car str-list-2)
              (string-merge (cdr str-list-1) (cdr str-list-2))))))   

(string-merge (list "a" "e") (list "b" "kat" "ten" "."))

"NEXT: String-merge. Iterative variant"

(define (string-merge-iter str-list-1 str-list-2)
 (merge-iter-helper  str-list-1 str-list-2 ""))

(define (merge-iter-helper str-list-1 str-list-2 res)
 (cond ((null? str-list-1) 
          (string-append res (apply string-append str-list-2)))
       ((null? str-list-2) 
          (string-append res (apply string-append str-list-1)))
       (else (merge-iter-helper
                (cdr str-list-1) 
                (cdr str-list-2)
                (string-append 
                    res (car str-list-1) (car str-list-2))))))

(string-merge-iter (list "a" "e") (list "b" "kat" "ten" "."))

"NEXT: STRING-OF-CHAR-LIST: ITERATIVE VARIANT"

(define (string-of-char-list? str char-list)
  (string-of-char-list-1? str char-list 0 (string-length str)))

(define (string-of-char-list-1? str char-list i lgt)
  (if (= i lgt)
      #t
      (and (memv (string-ref str i) char-list)
           (string-of-char-list-1? str char-list (+ i 1) lgt))))

(string-of-char-list? "abekat" (list #\a #\b #\e #\k  #\t))
(string-of-char-list? "abekat" (list #\a #\b))

"NEXT: EXPENSIVE RECURSIVE VARIANT"

(define (string-of-char-list? str char-list)
  (if (eqv? str "")
      #t
      (and (memv (string-ref str 0) char-list)
           (string-of-char-list? (substring str 1 (string-length str)) char-list))))

(string-of-char-list? "abekat" (list #\a #\b #\e #\k  #\t))
(string-of-char-list? "abekat" (list #\a #\b))

"NEXT: RECURSTION WITHOUT DEFINE OR LETREC:"

(let ((fac
         (lambda (n)
            (if (= n 1)
                1
                (* n (fac  (- n 1)))))))
  (fac 5)
)

((lambda (fac)
   (fac 5))
 (lambda (n)
   (if (= n 0) 1 (* n (fac  (- n 1)))))
)

; 3 different illustraton with letrec

(letrec ((fac (lambda (n)
                 (if (= n 0)
                     1
                     (* n (fac (- n 1)))))))
  (fac 5)
)

(let ((fac #f))
  (set! fac (lambda (n)
              (if (= n 0)
                  1
                  (* n (fac (- n 1))))))
  (fac 5)
)

; Self-passing idea:
(let ((fac (lambda (f n)
              (if (= n 0)
                  1
                  (* n (f f (- n 1)))))))
  (fac fac 5)
)

; Currying - compare to the final result using Y:
(let ((fac (lambda (f)
             (lambda (n)
               (if (= n 0)
                   1
                   (* n  ((f f) (- n 1))))))))
  ((fac fac) 5)
)

; Let rewritten to lambda
((lambda (fac) 
   ((fac fac) 5))
  (lambda (f)
    (lambda (n)
      (if (= n 0)
          1
          (* n  ((f f) (- n 1)))))))


; Introducing Y:
(let ((fac (Y (lambda (f)    
                (lambda (n) 
                   (if (= n 0) 
                       1
                       (* n (f (- n 1)))))))))
  (fac 5))

; Defining Y - as a mystery:
(define Y (lambda (j)
             (let ((i (lambda (f)               
                        (lambda (n)
                          ((j (f f)) n) ))))
               (i i))))

; Again:
(let ((fac (Y (lambda (f)    
                (lambda (n) 
                   (if (= n 0)
                       1
                       (* n (f (- n 1)))))))))
  (fac 5))

"THE END"   

Recursion Slide Annotated slide Contents Index References

Recursive functions are indispensable for the processing of recursive data structures

The concept recursion: Recursion is an algorithmic program solving idea that involves solution of subproblems of the same nature as the overall problem

Given a problem P If P is trivial then solve it immediately If P is non-trivial, divide P into subproblems P1 ,..., Pn Observe if Pi (i=1..n) are of the same nature as P If so, use the overall problem solving idea on each of P1 ... Pn Combine solutions of the subproblems P1 ... Pn to a solution of the overall problem P The problem solving technique sketched here is called divide and conquer. It is not all divide and conquer problems that involve recursion. But many do in fact. Recursion comes into play when the subproblems P1 ... Pn turn out to be of the same nature as the overall problem, and as such they can be solved by the same 'medicine' as used for the overall problem P.

Reference Foldoc: recursion

Recursion versus iteration Slide Annotated slide Contents Index References

Recursive functions are sufficient - but typically memory inefficient - for programming of an iterative process. Tail recursive functions in Scheme are memory efficient for programming of any iterative process.

The concept tail recursion: Tail recursion is a variant of recursion in which the recursive call takes place without contextual, surrounding calculations in the recursive function. In a tail recursion function the recursive call is a tail call (see next slide)

A tail call is the last 'thing' to be done before the function returns. Therefore there is no need to maintain any activation record of such a call - we can reuse the previous activation record. The image series below will illustrate this.

Image series: A recursive formulation of the function fak and the accompanying recursive process

A recursive formulation of the function fak and the accompanying recursive process

Image no. 1. The recursion is developed - activation records are stacked

 

Image no. 2. The recursion is developed - activation records are stacked

 

Image no. 3. The recursion is developed - activation records are stacked

 

Image no. 4. The recursion is developed - activation records are stacked

 

Image no. 5. The turning point is reached - now on to actual multiplication

 

Image no. 6. Trivial multiplication with 1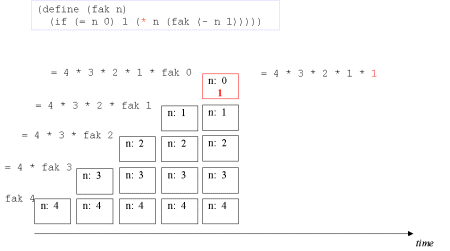

 

Image no. 7. Yet another time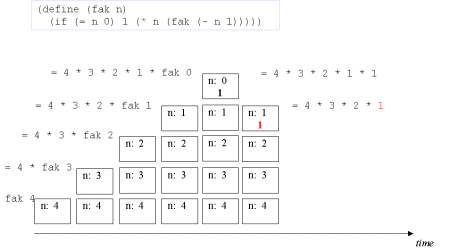

 

Image no. 8. Multiplication with 2

 

Image no. 9. Multiplication with 3

 

Image no. 10. Multiplication with 4

 

Image series: A tail recursive formulation of the function fak and the accompanying iterative process without memory optimization

A tail recursive formulation of the function fak and the accompanying iterative process without memory optimization

Image no. 1. The recursion develops - multiplication with 4

 

Image no. 2. The recursion develops - multiplication with 3

 

Image no. 3. The recursion develops - multiplication with 2

 

Image no. 4. The recursion develops - multiplication with 1

 

Image no. 5. Turning point - we have the result in r

 

Image no. 6. Non-productive unstacking

 

Image no. 7. Non-productive unstacking

 

Image no. 8. Non-productive unstacking

 

Image no. 9. Non-productive unstacking

 

Image no. 10. Non-productive unstacking

 

Image series: A tail recursive formulation of the function fak and the accompanying, memory optimized iterative process

A tail recursive formulation of the function fak and the accompanying, memory optimized iterative process

Image no. 1. Multiplication with 4

 

Image no. 2. Multiplication with 3 - frame reused

 

Image no. 3. Multiplication with 2 - frame reused

 

Image no. 4. Multiplication with 1 - frame reused

 

Image no. 5. Done - the result is in r

 

References R5RS: Proper tail recursion Foldoc: iteration Foldoc: recursion

Tail Calls Slide Annotated slide Contents Index References

A tail call of f in g occurs if g returns the result of f directly In Scheme, tail calls must be implemented efficiently as jumps - the stack frame of g is discarded when f is called Guy Steele: Tail calls are GOTOs with parameters

Program: Tail call.

(define (g ...) .... (f ...))

Program: Example of tail calls and non tail calls.

(define (a) (b) ; tail call ) (define (c condition) (if condition (d) ; tail call (e) ; tail call ) ) (define (f) (g ; tail call (h) ; non tail call (i) ; non tail call ) ) (define (j) (let ((n (k))) ; k is a non tail call (l n) ; a tail call ) )

References Wikipedia: Tail call R5RS: Proper tail recursion

Example of recursion: number-interval Slide Annotated slide Contents Index References

The function number-interval returns a list of integers from a lower bound to an upper bound

Program: The function number-interval from the general LAML library. This function returns a list of t-f+1 numbers from f to t .Try it out!.

(define (number-interval f t) (if (<= f t) (cons f (number-interval (+ f 1) t)) '()))

Program: The function number-interval-iter is an iterative, tail recursive variant of number-interval.

(define (number-interval-iter f t) (reverse (number-interval-iter-help f t '()))) (define (number-interval-iter-help f t res) (if (<= f t) (number-interval-iter-help (+ f 1) t (cons f res)) res))

Program: A sample dialogue with the number interval functions.

1> (number-interval 1 10) (1 2 3 4 5 6 7 8 9 10) 2> (number-interval-iter 10 20) (10 11 12 13 14 15 16 17 18 19 20) 3> (number-interval-iter 20 10) ()

Exercise 2.3. The append function

The function append, which is a standard Scheme function, concatenates two or more lists. Let us here show a version which appends two lists: (define (my-append lst1 lst2) (cond ((null? lst1) lst2) (else (cons (car lst1) (my-append (cdr lst1) lst2))))) We will now challenge ourselves by programming an iterative solution, by means of tail recursion. We start with the standard setup: (define (my-next-append lst1 lst2) (my-next-append-1 lst1 lst2 ...)) where my-next-append-1 is going to be the tail recursive function: (define (my-next-append-1 lst1 lst2 res) (cond ((null? lst1) ...) (else (my-next-append-1 (cdr lst1) lst2 ...)))) Fill out the details, and try out your solution. You may encounter a couple of problems! Do your best to work around these problems, maybe by changing aspects of the templates I have given above.

Exercise 2.3. A list replication function

Write a tail recursive function called replicate-to-length, which in a cyclic way (if necessary) replicates the elements in a list until the resulting list is of a certain exact length. You should think of replicate-to-length as a function that iterates over the elements of the list, repeatedly, if necessary. You will probably need to write a helping function to replicate-to-length, which is tail recursive. The following serves as an example: (replicate-to-length '(a b c) 8) => (a b c a b c a b) (replicate-to-length '(a b c) 2) => (a b) In other words, in (replicate-to-length lst n), take elements out of lst, cyclic if necessary, until you reach n elements.

Examples of recursion: string-merge Slide Annotated slide Contents Index References

The function string-merge zips two lists of strings to a single string. The lists are not necessarily of equal lengths

Program: The recursive function string-merge. Notice that this function is a general recursive function. The recursive call, emphasized above, is not in a tail position, because of the embedding in string-append.

(define (string-merge str-list-1 str-list-2) (cond ((null? str-list-1) (apply string-append str-list-2)) ((null? str-list-2) (apply string-append str-list-1)) (else (string-append (car str-list-1) (car str-list-2) (string-merge (cdr str-list-1) (cdr str-list-2))))))

Program: A tail recursive version of string-merge.

(define (string-merge-iter str-list-1 str-list-2) (merge-iter-helper str-list-1 str-list-2 "")) (define (merge-iter-helper str-list-1 str-list-2 res) (cond ((null? str-list-1) (string-append res (apply string-append str-list-2))) ((null? str-list-2) (string-append res (apply string-append str-list-1))) (else (merge-iter-helper (cdr str-list-1) (cdr str-list-2) (string-append res (car str-list-1) (car str-list-2))))))

Exercise 2.4. More about string-merge

We have seen two variants of string-merge on the accompanying slide. Both make use of (apply string-merge ...) in the cases where one of the lists become empty. apply calls a function on a list of parameters. Thus (apply + (list 1 2)) is equivalent to (+ 1 2). Eliminate the use of apply, such that string-merge (tail) recursively builds the end of the list by a number of calls to string-append (one for each element in the non-empty list).

Examples with recursion: string-of-char-list? Slide Annotated slide Contents Index References

The function string-of-char-list? is a predicate (a boolean function) that finds out if a string is formed exclusively by characters from a particular alphabet

Program: The function string-of-char-list? which relies on the tail recursive function string-of-char-list-1?. The function string-of-char-list-1? iterates through the characters in str, via the controlling parameters i and lst.

(define (string-of-char-list? str char-list) (string-of-char-list-1? str char-list 0 (string-length str))) (define (string-of-char-list-1? str char-list i lgt) (if (= i lgt) #t (and (memv (string-ref str i) char-list) (string-of-char-list-1? str char-list (+ i 1) lgt))))

Program: Applications of string-of-char-list?. The function blank-string? determines if a string is formed entirely of white space characters. The function numeric-string? is a predicate that returns true if the string consists exclusively of decimal digits. This is, for instance, useful to check the form input of dates and time in some server-based web applications. The version of numeric-string? in the lib/general.scm of LAML is slightly more general than the version shown above (it allows + or - signs as well, depending on an optional parameter).

;; A list of characters considered as blank space characters (define white-space-char-list (list #\space (as-char 13) (as-char 10) #\tab)) ;; Is the string str empty or blank (consists of white space) (define (blank-string? str) (or (empty-string? str) (string-of-char-list? str white-space-char-list))) ;; Returns if the string str is numeric. ;; More specifically, does str consist exclusively of the ;; ciffers 0 through 9. (define (numeric-string? str) (string-of-char-list? str (list #\0 #\1 #\2 #\3 #\4 #\5 #\6 #\7 #\8 #\9 )))

Exercises Slide Annotated slide Contents Index References

On this page we present an exercise related to recursive processing of lists

Exercise 2.7. Sublists of a list

The first part of this exercise is similar to an exercise from the previous lecture. In this exercise we will program a function front-sublist which returns the first n elements of a list. The signature (the head) of the function should be (front-sublist lst n) where lst is a list and n is a number. As a precondition it can be assumed that lst is a proper list and that n is a non-negative integer. As a postcondition we want to guarantee that the length of the result is n. As an example (front-sublist '(a b c d e) 3) => (a b c) (front-sublist '(a b c d e) 6) => ERROR First, identify the extreme, border cases and be sure that you know how to handle these. Next, program the function with due respect to both the precondition and the postcondition. Next, test the function carefully in a dialogue with your Scheme system. Given the function front-sublist we will program the function sublists, which breaks a proper list into a list of sublists of some given size. As an example (sublists '(a b c d e f) 3) => ((a b c) (d e f)) Program the function sublists with use of front-sublist. Be careful to prepare you solution by recursive thinking. It means that you should be able to break the overall problem into a smaller problem of the same nature, as the original problem. You should feel free to formulate both preconditions and postconditions of the function sublists, such that the existing function front-sublist fits well. Hint: The Scheme function list-tail is probably useful when you program the function sublists.

Exercise 2.7. A variant of number-interval

We have studied the function number-interval in this lecture (on this slide) and we have seen that (number-interval 10 1) evaluates to the empty list. Program a variant of number-interval such that (number-interval 10 1) evaluates to the list (10 9 8 7 6 5 4 3 2 1).

Exercise 2.7. A variant of string-of-char-list?

The function string-of-char-list? was programmed with use of a help function which we called string-of-char-list-1? on this slide. The help function was programmed side by side with string-of-char-list?. As an altertive, string-of-char-list-1? could be programmed as a local function of string-of-char-list? Please do that, using an appropriate name binding form. The help function keeps track of an index i in an additional parameter. It is possible to program string-of-char-list? without use of a help function. This function should iterate over shorter and shorter text strings. Please do that now. Consider the efficiency of this function and our original version of string-of-char-list?. (The function substring is useful).

It is not straightforward to program a recursive function in Scheme - using just lambda

Program: A naive attempt to define a recursive function.

(let ((fac (lambda (n) (if (= n 1) 1 (* n (fac (- n 1))))))) (fac 5) ) ; reference to undefined identifier: fac

Program: Equivalent to the program above.

((lambda (fac) (fac 5)) (lambda (n) (if (= n 0) 1 (* n (fac (- n 1))))) ) ; reference to undefined identifier: fac

Program: A definition of fac with letrec.

(letrec ((fac (lambda (n) (if (= n 0) 1 (* n (fac (- n 1))))))) (fac 5)) ; OK: 120

Program: Equivalent to the program above - notice the use of assignment.

(let ((fac #f)) (set! fac (lambda (n) (if (= n 0) 1 (* n (fac (- n 1)))))) (fac 5)) ; OK. 120

Program: Passing fac to itself - the key to a solution.

(let ((fac (lambda (f n) (if (= n 0) 1 (* n (f f (- n 1))))))) (fac fac 5)) ; 120

We now wish to separate the factorial stuff and the self passing stuff This involves a number of steps - each of which are simple - but the resulting self passing stuff ends up being complicated

Development of the Y-combinator Slide Annotated slide Contents Index References

We do a step-wise development that leads to the Y-combinator - following the trail devised by Richard Gabriel in The Why of Y.

Reference Richard Gabrial: The why of Y

Program: Wishful thinking - the goal of our work: Generating a recursive factorial function from an almost recursive factorial function.

(let ((recursive-factorial (Y (lambda (???) (lambda (n) (if (= n 0) 1 (* n (??? (- n 1))))))))) (recursive-factorial 5)) ; ??? is just a name. But what is Y?

Program: The starting point - again.

; The starting point. (let ((fac (lambda (f n) ; CURRY (lambda (f n) ...) (if (= n 0) 1 (* n (f f (- n 1))))))) (fac fac 5))

Program: After simple currying.

; Just currying (lambda (f (lambda (n) ...))). Not better - perhaps even worse... (let ((fac (lambda (f) (lambda (n) (if (= n 0) 1 (* n ((f f) (- n 1)))))))) ; GET RID OF (f f) ((fac fac) 5)) ; BY ABSTRACTING IT OUT OF THE IF-FORM.

Program: Abstracting (f f) out of if.

; We wish to preserve the recusive form of factorial as much as possible. ; Therefore getting rid of (f f) in (lambda (n) ....) ; Abstracting if to get rid of (f f). (let ((fac (lambda (f) ; THE NAME fac IS NOW MISLEADNIG (lambda (n) (let ((g (lambda (h) (if (= n 0) 1 (* n (h (- n 1))))))) (g (f f))) )))) ((fac fac) 5))

Program: After a simple renaming of fac to i.

; Now misleadning to use the name fac. Use the name i instead: (let ((i (lambda (f) (lambda (n) (let ((g (lambda (h) ; NOW PASS n AS PARAMETER TO (lambda (h) ...) (if (= n 0) 1 (* n (h (- n 1))))))) (g (f f))) )))) ((i i) 5))

Program: Introducing n as parameter to (lambda (h) ...).

; Passing n as parameter instead of relying on outer n. As a preparation to tear things appart... (let ((i (lambda (f) (lambda (n) (let ((g (lambda (h n) ; NEXT CURRY IT (if (= n 0) 1 (* n (h (- n 1))))))) (g (f f) n)) )))) ((i i) 5))

Program: After currying.

; Currying again: (let ((i (lambda (f) (lambda (n) (let ((g (lambda (h) ; THE LAMBDA EXPRESSION BOUND TO g HAS NO FREE VARIABLES (lambda (n) ; MOVET IT OUT (if (= n 0) 1 (* n (h (- n 1)))))))) ((g (f f)) n)) )))) ((i i) 5))

Program: The lambda expression bound to g has been moved out.

; g is now at the outer level. (let ((g (lambda (h) (lambda (n) (if (= n 0) 1 (* n (h (- n 1)))))))) (let ((i (lambda (f) (lambda (n) (let () ; NOW GET RID OF EMPTY let ((g (f f)) n)) )))) ((i i) 5)))

Program: Empty let removed.

; Getting rid of empty let - a small step... (let ((g (lambda (h) ; g is our factorial form (lambda (n) (if (= n 0) 1 (* n (h (- n 1)))))))) (let ((i (lambda (f) ; here is the bookkeeping stuff (lambda (n) ((g (f f)) n) )))) ; HERE g IS BOUND TO MEANING AT OUTER LEVEL ((i i) 5))) ; PASS IT VIA A PARAMETER INSTEAD

Program: Introduce function for (let ((i ..)) ...).

; We wish that the (let ((i ...))) form is a function to which g is passed as parameter. (let ((g (lambda (h) (lambda (n) (if (= n 0) 1 (* n (h (- n 1)))))))) ((lambda (j) (let ((i (lambda (f) (lambda (n) ((j (f f)) n) )))) ((i i) 5))) ; THE NUMBER 5 DOES NOT BELONG TO g)) ; THE SELF APPLICATION STUFF. MOVE IT OUT.

Program: A small but irritating detail. Get 5 out the self application stuff.

; Get 5 out of (lambda (g) ...) (let ((g (lambda (h) (lambda (n) (if (= n 0) 1 (* n (h (- n 1)))))))) (((lambda (j) ; NOW FACTOR OUT (lambda (j) ...) (let ((i (lambda (f) ; TO A NAMED FUNCTION Y (lambda (n) ((j (f f)) n) )))) (i i))) g) 5))

Program: Factoring self application stuff out. Call it Y.

; Factor out Y. (define Y (lambda (j) (let ((i (lambda (f) (lambda (n) ((j (f f)) n) )))) (i i)))) (let ((g (lambda (h) (lambda (n) (if (= n 0) 1 (* n (h (- n 1)))))))) ((Y ; NOW PASS the value of g DIRECTLY TO Y g) 5))

Program: The end result.

; Bind (G y) to fac. The end result. (define Y (lambda (j) (let ((i (lambda (f) (lambda (n) ((j (f f)) n) )))) (i i)))) (let ((fac (Y (lambda (h) (lambda (n) (if (= n 0) 1 (* n (h (- n 1))))))))) (fac 5)) ; We are done!

The concept higher-order function: A higher-order function accepts functions as arguments and/or is able to return a function as its result
The concept higher-order language: A higher-order language supports higher-order functions and allows functions to be constituents of data structures

The order of data Order 0: Non function data Order 1: Functions with domain and range of order 0 Order 2: Functions with domain and range of order 1 Order k: Functions with domain and range of order k-1 Order 0 data have nothing to do with functions. Numbers, lists, and characters are example of such data. Data of order 1 are functions which work on 'ordinary' order 0 data. Thus order 1 data are the functions we have been concerned with until now. Data of order 2 - and higher - are example of the functions that have our interest in this lecture.

Functions of order i, i >= 2, are called higher-order functions

Some simple and general higher-order functions Slide Annotated slide Contents Index References

It is time to look at some examples of higher-order functions. We start with a number of simple ones.

We show three small, but useful higher-order functions

Program: The function flip changes the order of it's parameters. The function takes a function of two parameters, and returns another function of two parameters. The only difference between the input and output function of flip is the ordering of their parameters.

(define (flip f) (lambda (x y) (f y x)))

Program: An alternative formulation of flip without use of the sugared define syntax. For easy comparison we show the original version below the alternative formulation. The two different syntaxes are discussed in an earlier lecture, cf. the cross references.

(define flip (lambda (f) (lambda (x y) (f y x)))) (define (flip f) (lambda (x y) (f y x)))

Program: The function negate negates a predicate. Thus, negate takes a predicate function (boolean function) as parameter and returns the negated predicate. The resulting negated predicate returns true whenever the input predicate returns false, and vise versa.

(define (negate p) (lambda (x) (if (p x) #f #t)))

Program: The function compose composes two functions which both are assumed to take a single argument. The resulting function composed of f and g returns f(g(x)), or in Lisp (f (g x)), given the input x . The compose function from the general LAML library accepts two or more parameters, and as such it is more general than the compose function shown here.

(define (compose f g) (lambda (x) (f (g x))))

Exercise 2.8. Using flip, negate, and compose

Define and play with the functions flip, negate, and compose, as they are defined on this page . Define, for instance, a flipped cons function and a flipped minus function. Define the function odd? in terms of even? and negate. Be sure you understand your results.

Reference The syntax of function definition

Linear search in lists Slide Annotated slide Contents Index References

Search criterias can be passed as predicates to search functions

Program: A linear list search function. A predicate accepts as input an element in the list, and it returns either true (#t) or false (#f). If the predicate holds (if it returns true), we have found what we searched for. The predicate pred is passed as the first parameter to find-in-list. As it is emphasized in blue color, the predicate is applied on the elements of the list. The first successful application (an application with true result) terminates the search, and the element is returned. If the first case in the conditional succeeds (the brown condition) we have visited all elements in the list, and we conclude that the element looked for is not there. In that case we return false.

;; A simple linear list search function. ;; Return the first element which satisfies the predicate pred. ;; If no such element is found, return #f. (define (find-in-list pred lst) (cond ((null? lst) #f) ((pred (car lst)) (car lst)) (else (find-in-list pred (cdr lst)))))

Program: A sample interaction using find-in-list. We define a simple association list which relates persons (symbols) and hair colors (strings). The third interaction searches for per's entry in the list. The fourth interaction searches for a person with pink hair color. In the fifth interaction nothing is found, because no person has yellow hair color. In the sixth interaction we illustrate the convenience of boolean convention in Scheme: everything but #f counts as true. From a traditional typing point of view the let expression is problematic, because it can return either a person (a symbol) or a boolean value. Notice however, from a pragmatic point of view, how useful this is.

1> (define hair-colors (pair-up '(ib per ann) '("black" "green" "pink"))) 2> hair-colors ((ib . "black") (per . "green") (ann . "pink")) 3> (find-in-list (lambda (ass) (eq? (car ass) 'per)) hair-colors) (per . "green") 4> (find-in-list (lambda (ass) (equal? (cdr ass) "pink")) hair-colors) (ann . "pink") 5> (find-in-list (lambda (ass) (equal? (cdr ass) "yellow")) hair-colors) #f 6> (let ((pink-person (find-in-list (lambda (ass) (equal? (cdr ass) "pink")) hair-colors))) (if pink-person (car pink-person) #f)) ann

Exercise 2.13. Linear string search

Lists in Scheme are linear linked structures, which makes it necessary to apply linear search techniques. Strings are also linear structures, but based on arrays instead of lists. Thus, strings can be linearly searched, but it is also possible to access strings randomly, and more efficiently. First, design a function which searches a string linearly, in the same way as find-in-list. Will you just replicate the parameters from find-in-list, or will you prefer something different? Next program your function in Scheme.

Exercise 2.13. Index in list

It is sometimes useful to know where in a list a certain element occurs, if it occurs at all. Program the function index-in-list-by-predicate which searches for a given element. The comparison between the given element and the elements in the list is controlled by a comparison parameter to index-in-list-by-predicate. The function should return the list position of the match (first element is number 0), or #f if no match is found. Some examples will help us understand the function: (index-in-list-by-predicate '(a b c c b a) 'c eq?) => 2 (index-in-list-by-predicate '(a b c c b a) 'x eq?) => #f (index-in-list-by-predicate '(two 2 "two") 2 (lambda (x y) (and (number? x) (number? y) (= x y)))) => 1 Be aware if your function is tail recursive.

Exercise 2.13. Binary search in sorted vectors

Linear search, as illustrated by other exercises, is not efficient. It is often attractive to organize data in a sorted vector, and to do binary search in the vector. This exercise is meant to illustrate a real-life higher-order function, generalized with several parameters that are functions themselves. Program a function binary-search-in-vector, with the following signature: (binary-search-in-vector v el sel el-eq? el-leq?) v is the sorted vector. el is the element to search for. If v-el is an element in the vector, the actual comparison is done between el and (sel v-el). Thus, the function sel is used as a selector on vector elements. Equality between elements is done by the el-eq? function. Thus, (el-eq? (sel x) (sel y)) makes sense on elements x and y in the vector. The ordering of elements in the vector is defined by the el-leq? function. (el-leq? (sel x) (sel y)) makes sense on elements x and y in the vector. The call (binary-search-in-vector v el sel el-eq? el-leq?) searches the vector via binary search and it returns an element el-v from the vector which satisfies (el-eq? (sel el-v) el). If no such element can be located, it returns #f. Here are some examples, with elements being cons pairs: (binary-search-in-vector '#( (2 . x) (4 . y) (5 . z) (7 . i) (9 . c) (11 . c)) 7 car = <=) => (7 . i) (binary-search-in-vector '#( (2 . x) (4 . y) (5 . z) (7 . i) (9 . c) (11 . c)) 2 car = <=) => (2 . x) (binary-search-in-vector '#( (2 . x) (4 . y) (5 . z) (7 . i) (9 . c) (11 . c)) 10 car = <=) => #f Be sure to program a tail recursive solution.

Exercise 2.13. Generating a C-style compare function

A C-style compare function (cmp x y) returns -1 if x is less than y, 0 if x is equal to y, and 1 if x is greater than y. Write a higher-order function make-comparator, that takes two functions lt (less than) and gt (greater than) as parameters and generates a C-style compare function. With a little more thought we can generate a C-style compare function from only the function lt. Give it a try. Use make-comparator and a standard function string<? to generate a function that compares two strings in a C-style (a Scheme version of strcmp). The other way around, write a higher-order function that takes a C-style compare function and generates a list of functions: lt, equal, gt. Test each of the three generated functions and make sure they work as expected.

Exercise 2.13. Higher-order functions in 'Functional Programming Languages'

A number of short papers appeared in 1996 in the journal Computing Surveys (as part of the 50 years celebration of the ACM) - among them a paper titled 'Functional Programming Languages' by Benjamin Goldberg. Take a brief look at the paper - in particular the section about 'Higher-order functions'. It is an easy paper to read. Rewrite the functions prod, fac, and power in Scheme, and give them a try. Do you get the results you would expect? If not, carry out the necessary corrections. The product operator is introduced to improve the recursive factorial function, suposedly in the direction of iteration. However, the paper is not successful in that respect. Why? Write an iterative, memory efficient, tail-recursive version of prod in Scheme.

Generation of list selectors Slide Annotated slide Contents Index References

It is attractive to generate generalizations of the list selector functions car, cadr, etc

Program: A simple version of the make-selector-function function.

(define (make-selector-function n) (lambda (lst) (list-ref lst (- n 1))))

Program: The existing LAML make-selector-function. It is crucial that you get good error messages in case you access a non-existing list component. This version handles this. For error messages purposes this version of the function accepts an optional parameter, which (somehow redundantly) gives the name of the selector function.

;; Returns a function, which selects element number n in a list. ;; The second parameter, which is optional, is used for error message purposes. ;; In general, this parameter should be a string corresponding to the name of the selector function. ;; If the second parameter is given, we check whether the list is long enough for selection. ;; If not, we give a decent error message. We recommend use of the second parameter in order to ;; avoid meaningless error messages. ;; The first element is number 1. ;; (make-selector-function 1) corresponds to car, (make-selector-function 2) corresponds to cadr, etc. ;; .form (make-selector-function n [selector-name]) (define (make-selector-function n . optional-parameter-list) (let ((selector-name (optional-parameter 1 optional-parameter-list #f))) (if selector-name (lambda (lst) (let ((lgt (length lst))) (if (> n lgt) (display-error (string-append "The selector function " (as-string selector-name) ": " "The list " (as-string lst) " is is too short for selection. " "It must have at least " (as-string n) " elements." )) (list-ref lst (- n 1))))) (lambda (lst) (list-ref lst (- n 1))))))

Program: Example usages of the function make-selector-function. In interaction 1 through 3 we demonstrate generation and use of the first function. Next we outline how to define accessors of data structures, which are represented as lists. In reality, we are dealing with list-based record structures. In my every day programming, such list structures are quite common. It is therefore immensely important, to access data abstractly (via name accessors, instead of via the position in the list (car, cadr, etc). In this context, the make-selector-function comes in handy.

1> (define first (make-selector-function 1 "first")) 2> (first '(a b c)) a 3> (first '()) The selector function first: The list () is is too short for selection. It must have at least 1 elements. > 4> (define (make-person-record firstname lastname department) (list 'person-record firstname lastname department)) 5> (define person-record (make-person-record "Kurt" "Normark" "Computer Science")) 6> (define first-name-of (make-selector-function 2 "first-name-of")) 7> (define last-name-of (make-selector-function 3 "last-name-of")) 8> (last-name-of person-record) "Normark" 9> (first-name-of person-record) "Kurt"

Apply Slide Annotated slide Contents Index References

The function apply calls a function on a list of parameters

Program: Sample usage of apply.

> (+ 1 2 3 4) 10 > (+ (list 1 2 3 4)) +: expects argument of type <number>; given (1 2 3 4) > (apply + (list 1 2 3 4)) 10 > (reverse (list 1 2 3 4)) (4 3 2 1) > (reverse 1 2 3 4) reverse: expects 1 argument, given 4: 1 2 3 4 > (apply reverse (list 1 2 3 4)) reverse: expects 1 argument, given 4: 1 2 3 4 > (define (reverse-1 . x) (reverse x)) > (reverse-1 1 2 3 4) (4 3 2 1) > (apply reverse-1 (list 1 2 3 4)) (4 3 2 1)

"NEXT: Introduction to higher-order functions: flip"

(define (flip f)
  (lambda (x y)
    (f y x)))

(define flip
  (lambda (f)
    (lambda (x y)
      (f y x))))

(- 5 6)
((flip -) 5 6)
(cons 5 6)
((flip cons) 5 6)

"NEXT: Introduction to higher-order functions: negate"

(define (negate p)
  (lambda (x) 
    (not (p x))))

(define (is-even? x)
  (= (remainder x 2) 0))

(is-even? 5)
(is-odd? 5)

(define is-odd? (negate is-even?))
(is-odd? 5)

(< 5 6)
((negate <) 5 6)   ; UPS...

(define (negate p)
  (lambda x
    (not (apply p x))))

((negate <) 5 6)

"NEXT: compose"

(define (compose f g)
  (lambda (x)
    (f (g x))))

((compose is-even? (lambda (x) (* 2 x))) 3)

(define ff 
  (compose 
     (lambda (x) (* x x))
     (lambda (x) (+ x 1))))

(ff 5)

"NEXT: Linear search: find-in-list"

(define (find-in-list pred lst)
  (cond ((null? lst) #f)
        ((pred (car lst)) (car lst))
        (else (find-in-list pred (cdr lst)))))

(define lst (list #f 6.7 5 (cons 5 6) #\a (lambda(x) (* x 2))))

(find-in-list integer? lst)
(find-in-list real? lst)
(find-in-list boolean? lst)
(find-in-list pair? lst)
(find-in-list char? lst)
(find-in-list procedure? lst)

"NEXT: Selector functions: first, second, third, .."

(define (make-selector-function n)
  (lambda (lst) (list-ref lst (- n 1))))

(define first  (make-selector-function 1))
(define second (make-selector-function 2))
(define third  (make-selector-function 3))

(let ((lst (list 1 2 3 4 5)))
  (list (third lst) (second lst) (first lst)))


"NEXT: Mapping and filtering"

(define (mymap f lst)
  (if (null? lst)
      '()
      (cons (f (car lst))
            (mymap f (cdr lst)))))

(mymap is-even? (list 1 2 3 4 5 6 7))
(mymap (lambda (x) (* x 2)) (list 1 2 3 4 5 6 7))

(map is-even? (list 1 2 3 4 5 6 7))
(map (lambda (x) (* x 2)) (list 1 2 3 4 5 6 7))

(define (myfilter p lst)
  (cond ((null? lst) lst)
        ((p (car lst)) (cons (car lst) (myfilter p (cdr lst))))
        (else (myfilter p (cdr lst)))))

(myfilter is-even? (list 1 2 3 4 5 6 7 8))
(myfilter (negate is-even?) (list 1 2 3 4 5 6 7 8))

(define (iterative-filter pred lst)
  (reverse (filter-help pred lst '())))

(define (filter-help pred lst res)
  (cond ((null? lst) res)
        ((pred (car lst)) 
           (filter-help pred (cdr lst)  (cons (car lst) res)))
        (else 
           (filter-help pred (cdr lst)  res))))

(iterative-filter is-even? (list 1 2 3 4 5 6 7 8))
(iterative-filter (negate is-even?) (list 1 2 3 4 5 6 7 8))


"NEXT: Reduction and accumulation"

(reduce-right - (list 1 2 3 4 5))  ; undefined
(- 1 (- 2 (- 3 (- 4 5))))

(define (reduce-right f lst)
  (if (null? (cdr lst))
      (car lst)
      (f (car lst) 
         (reduce-right f (cdr lst)))))

(reduce-right - (list 1 2 3 4 5))
(reduce-right - (list 1))
(reduce-right - (list))

(reduce-left - (list 1 2 3 4 5))
(- (- (- (- 1 2) 3) 4) 5)

(define (reduce-left f lst)
  (reduce-help-left f (cdr lst) (car lst)))

(define (reduce-help-left f lst res)
  (if (null? lst)
      res
      (reduce-help-left f (cdr lst) (f res (car lst)))))

(reduce-left - (list 1 2 3 4 5))

(define (reduce-left f lst)  ; All in one
  (letrec ((reduce-help-left
             (lambda (f lst res)
                (if (null? lst)
                    res
                   (reduce-help-left f (cdr lst) (f res (car lst)))))))
    (reduce-help-left f (cdr lst) (car lst))))

(reduce-left - (list 1 2 3 4 5))
(reduce-left - (list 1))
(reduce-left - (list))


(define (accumulate-right f init lst)
  (if (null? lst)
      init
      (f (car lst) (accumulate-right f init (cdr lst)))))

(accumulate-right - 0 (list 1 2 3 4 5))
(accumulate-right - 0 (list 1))
(accumulate-right - 0 (list))

"NEXT: zip"

(define (zip z lst1 lst2)
  (if (null? lst1)
      '()
      (cons 
        (z (car lst1) (car lst2))
        (zip z (cdr lst1) (cdr lst2)))))

(zip cons (list 1 2 3) (list 'a 'b 'c))

"NEXT: Currying"

(define (curry2 f)
  (lambda(x)
    (lambda(y)
      (f x y))))

(- 1 2)
(((curry2 -) 1) 2)

(define (curry3 f)
  (lambda(x)
    (lambda(y)
      (lambda(z)
       (f x y z)))))

(- 1 2 3)
((((curry3 -) 1) 2) 3)

(define (uncurry2 f)
  (lambda (x y)
    ((f x) y)))

((uncurry2 (curry2 -)) 1 2)

(define (uncurry3 f)
  (lambda (x y z)
    (((f x) y) z)))


"NEXT: Continuation passing style"

(define (p-direct a b)
  (* (+ a b) (- a b)))

(p-direct 5 10)

(define (p-cps a b k0)
  (plus a b (lambda(v1)
              (sub a b (lambda(v2)
                         (mult v1 v2 k0))))))

(define (plus a b k) (k (+ a b )))
(define (sub a b k)  (k (- a b)))
(define (mult a b k) (k (* a b)))

(p-cps 5 10 (lambda (x) x))

(define (fact-direct n)
  (if (= n 0)
      1
      (* n (fact-direct (- n 1)))))

(fact-direct 5)

(define (fact-cps n k)
  (if (= n 0)
      (k 1)
      (fact-cps (- n 1)
                (lambda(v)       ; Eventually v becomes (fact (- n 1)). 
                  (k (* n v)))   ; Now pass (* n v) = (* n (fact (- n 1))) to k.
      )
  )
)

(fact-cps 5 (lambda (x) x))

(define (fact-tail-rec n r)
  (if (= 0 n)
      r
      (fact-tail-rec (- n 1) (* r n))))

(fact-tail-rec 5 1)

(define (fact-tail-rec-cps-1 n r k)
  (if (= 0 n)
      (k r)
      (fact-tail-rec-cps-1
        (- n 1)
        (* r n)
        (lambda (v)  ; Eventually v becomes (fact n), because the base case passes 
           (k v))    ; the result via a chain of trivial "pass on" functions.
                     ; Are all these (lambda(v) (k v)) functions really necessary?
      )              ; No - see the next variant called fact-tail-rec-cps-2.
  )
)

(fact-tail-rec-cps-1 5 1 (lambda (x) x))

(define (fact-tail-rec-cps-2 n r k)
  (if (= 0 n)
      (k r)
      (fact-tail-rec-cps-2
        (- n 1)
        (* r n)
        k           ; Eventually (fact n) is passed to k. k is the continuation 
      )             ; of the original call to the factorial function.
   )
)

(fact-tail-rec-cps-2 5 1 (lambda (x) x))

"NEXT: list-length"

(define (list-length lst)
   (cond ((null? lst) 0)
         ((pair? lst) (+ 1 (list-length (cdr lst))))
         (else 'improper-list)))

(list-length '(a b c))
(list-length '(a b c . d))

(define (list-length-direct lst)
  (call-with-current-continuation
   (lambda (do-exit)
     (letrec ((list-length-inner
                (lambda (lst)
                   (cond ((null? lst) 0)
                         ((pair? lst) (+ 1 (list-length-inner (cdr lst))))
                         (else (do-exit 'improper-list))))))
       (list-length-inner lst)))  ))

(list-length-direct '(a b c . d))

(define (list-length-cps lst k0)    ; Now CPS. k0 is the outer continuation - ready to catch exceptional values
  (letrec ((list-length-inner
             (lambda (lst k1) 
               (cond ((null? lst) (k1 0))
                     ((pair? lst) (list-length-inner
                                    (cdr lst)
                                    (lambda (v) (k1 (+ 1 v))) ; v is the length of (cdr l).
                                                              ; Pass 1+v to k1.
                                )
                     )
                     (else (k0 'improper-list)))) ))         ; Pass the symbol improper-list
                                                             ; to the outer continuation k0.
    (list-length-inner lst k0)))

(list-length-cps '(a b c . d) (lambda (x) x))

(define (list-length-iter-cps lst res k0)  ; CPS, but now iterative, tail-recursive.
  ; k0 is passed along the tail recursive calls, and
  ; can also be used for passing 'an exceptional value'.
  (cond ((null? lst) (k0 res))
        ((pair? lst) (list-length-iter-cps (cdr lst) (+ res 1) k0))
        (else (k0 'improper-list))))

(list-length-iter-cps '(a b c . d) 0 (lambda (x) x))
(list-length-iter-cps '(a b c d) 0 (lambda (x) x))

"THE END"

Classical higher-order functions: Overview Slide Annotated slide Contents Index References

We start with an overview of the classical higher-order functions on lists, not just mapping and filtering, but also including reduction and zipping functions which we cover in subsequent sections.

There exists a few higher-order functions via which a wide variety of problems can be solved by simple combinations

Overview: Mapping: Application of a function on all elements in a list Filtering: Collection of elements from a list which satisfy a particular condition Accumulation: Pair wise combination of the elements of a list to a value of another type Zipping: Combination of two lists to a single list

The functions mentioned above represent abstractions of algorithmic patterns in the functional paradigm The idea of patterns has been boosted in the recent years, not least in the area of object-oriented programming. The classical higher-order list functions encode recursive patterns on the recursive data type list. As a contrast to many patterns in the object-oriented paradigm, the patterns encoded by map, filter, and others, can be programmed directly. Thus, the algorithmic patterns we study here are not design patterns. Rather, they are programming patterns for the practical functional programmer.

Mapping Slide Annotated slide Contents Index References

The idea of mapping is to apply a function on each element of a list, hereby collecting the list of the function applications

A mapping function m applies a function on each element of a list (e1, e2, ... en) The mapping functions returns the list of these applications

Figure. Mapping a function m on a list. m is applied on every element, and the list of these applications is returned.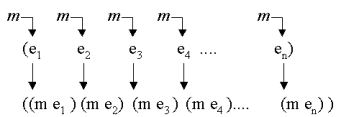

Reference Foldoc: map

The function map is an essential Scheme function

The mapping function Slide Annotated slide Contents Index References

It is now time to study the implementation of the mapping function. We program a function called mymap in order not to redefine Scheme's own mapping function (a standard function in all Scheme implementations).

We show a simple implementation of map - called mymap

Program: An implementation of map. This is not a good implementation because the recursive call is not a tail call. We leave it as an exercise to make a memory efficient implementation with tail recursion - see the exercise below.

(define (mymap f lst) (if (null? lst) '() (cons (f (car lst)) (mymap f (cdr lst)))))

Exercise 2.15. Iterative mapping function

In contrast to the function mymap on this page , write an iterative mapping function which is tail recursive. Test your function against mymap on this page, and against the native map function of your Scheme system.

Exercise 2.15. Table exercise: transposing, row elimination, and column elimination.

In an earlier section we have shown the application of some very useful table manipulation functions. Now it is time to program these functions, and to study them in further details. Program the functions transpose, eliminate-row, and eliminate-column, as they have been illustrated earlier. As one of the success criteria of this exercise, you should attempt to use higher-order functions as much and well as possible in your solutions. Hint: Program a higher-order function, (eliminate-element n). The function should return a function which eliminates element number n from a list.

Examples of mapping Slide Annotated slide Contents Index References

We will now study a number of examples.

Table. In the first row we map the string? predicate on a list of atoms (number, symbols, and strings). This reveals (in terms of boolean values) which of the elements that are strings. In the second row of the table, we map a 'multiply with 2' function on a list of numbers.

Expresion Value (map string? (list 1 'en "en" 2 'to "to")) (#f #f #t #f #f #t) (map (lambda (x) (* 2 x)) (list 10 20 30 40)) (20 40 60 80)

Filtering Slide Annotated slide Contents Index References

As the name indicates, the filter function is good for examining elements of a list for a certain property. Only elements which possess the property are allowed through the filter.

A filtering function applies a predicate (boolean function) f on every element of a list. Only elements on which the predicate returns true are returned from the filtering function.

Figure. Filtering a list with a predicate f. The resulting list is the subset of the elements which satisfy f (the elements on which f returns true).

Reference Foldoc: filter

The function filter is not an essential Scheme function

The filtering function Slide Annotated slide Contents Index References

The next item on the agenda is an implementation of filter .

For practical purposes it is important to have a memory efficient filter function

Program: An implementation of filter which is memory efficient. If the predicate holds on an element of the list (the red fragment) we include the element in the result (the brown fragment). If not (the green fragment), we drop the element from the result (the purple fragment).

(define (filter pred lst) (reverse (filter-help pred lst '()))) (define (filter-help pred lst res) (cond ((null? lst) res) ((pred (car lst)) (filter-help pred (cdr lst) (cons (car lst) res))) (else (filter-help pred (cdr lst) res))))

Exercise 2.16. A straightforward filter function

The filter function illustrated in the material is memory efficient, using tail recursion. Take a moment here to implement the straightforward recursive filtering function, which isn't tail recursive.

Examples of filtering Slide Annotated slide Contents Index References

As we did for mapping, we will also here study a number of examples. As before, we arrange the examples in a table where the example expressions are shown to the left, and their values to the right.

Table. In the first row we filter the first five natural numbers with the even? predicate. In the second row, we filter the same list of numbers with the odd? predicate. Rather than using the name odd? we form it by calculating (negate even?) . We have seen the higher-order function negate earlier in this lecture.

Expression Value (filter even? '(1 2 3 4 5)) (2 4) (filter (negate even?) '(1 2 3 4 5)) (1 3 5)

Reduction of a list by means of a binary operator transforms the list to a value in the range of the binary operator.

Figure. Left and right reduction of a list. Left reduction is - quite naturally - shown to the left, and right reduction to the right.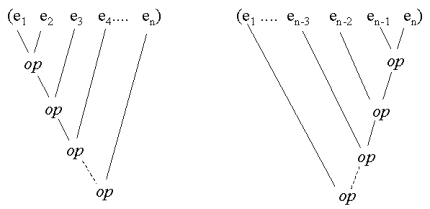

There is no natural value for reduction of the empty list. Therefore we assume as a precondition that the list is non-empty.

The reduction functions Slide Annotated slide Contents Index References

The function reduce-right is a straightforward recursive function The function reduce-left is a straightforward iterative function

Program: The function reduce-right. Notice the fit between the composition of the list and the recursive pattern of the right reduction.

Program: The function reduce-left. There is a misfit between left reduction and the recursive composition of the list with heads and tails. However, an iterative process where we successively combine e1 and e2 (giving r1 as the result), r1 and e3 etc., is straightforward. As we have seen several times, this can be done by a tail recursive function, here reduce-help-left.

Table. Examples of reductions. The - left reduction of the list corresponds to calculating the expression (- (- (- (- 1 2) 3) 4) 5). The - right reduction of the list corresponds to calculating the expression (- 1 (- 2 (- 3 (- 4 5)))).

Expression Value (reduce-left - '(1 2 3 4 5)) -13 (reduce-right - '(1 2 3 4 5)) 3 (reduce-left string-append (list "The" " " "End")) "The End" (reduce-left append (list (list 1 2 3) (list 'a 'b 'c))) (1 2 3 a b c)

Exercise 2.17. Quantifier Functions

The mathematical quantifiers for all and there exists are well-known. In this exercise we will write similar Scheme quantifier functions. The function (for-all lst p) is supposed to check if all elements in the list lst satisfy the predicate p. The function (there-exists lst p) is supposed to check if one or more elements in the list lst satisfy the predicate p. Finally, the function (there-exists-1 lst p) is supposed to check if exactly on element in the list lst satisfies p. Program and test these functions. You should in addition consider how to program these function by use of map, filter, and reduction (accumulation). Please decide if your functions are tail recursive.

Accumulation Slide Annotated slide Contents Index References

It is not satisfactory that we cannot reduce the empty list We remedy the problem by passing an extra parameter to the reduction functions We call this variant of the reduction functions for accumulation

Program: The function accumulate-right. The recursive pattern is similar to the pattern of reduce-right.

Table. Examples of right accumulations. The first row illustrates that we can accumulate the empty list. The second and third rows are similar to the second and third rows in Table 15.1.

Expression Value (accumulate-right - 0 '()) 0 (accumulate-right - 0 '(1 2 3 4 5)) 3 (accumulate-right append '() (list (list 1 2 3) (list 'a 'b 'c))) (1 2 3 a b c)

Zipping Slide Annotated slide Contents Index References

Two equally long lists can be pair wise composed to a single list by means of zipping them

Figure. Zipping two lists with the function z. The head of the resulting list is (z e i f i), where the element e i comes from the first list, and f i comes from the other.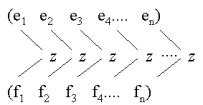

The zipping function Slide Annotated slide Contents Index References

Program: The function zip.

Table. Examples of zipping. Please notice that (map cons '(1 2 3) '(a b c)) gives the same result as provide that that map accept more than one list. The map in R5RS or R6RS does accept more than one list. If two lists are provided the mapping functions expects two parameters, one from each of the list.

Expression Value (zip cons '(1 2 3) '(a b c)) ((1 . a) (2 . b) (3 . c)) (apply string-append (zip string-append '("Rip" "Rap" "Rup") '(", " ", and " ""))) "Rip, Rap, and Rup" (string-merge '("Rip" "Rap" "Rup") '(", " ", and ")) "Rip, Rap, and Rup"

Reference The string-merge function

The concept currying: Currying allows us to understand every function as taking at most one parameter. Currying can be seen as a way of generating intermediate functions which accept additional parameters to complete a calculation

Figure. The signatures of curried functions. In the upper frame we show the signature of a function f, which takes three parameters. The frames below show the signature when f is curried. In the literature, the notation shown to the bottom right is most common. The frame to the left shows how to parse the notation (the symbol -> associates to the right).

Currying and Scheme is not related to each other. Currying must be integrated at a more basic level to be elegant and useful

Reference Foldoc: curried function

Currying in Scheme Slide Annotated slide Contents Index References

It is possible to generate curried functions in Scheme. But the parenthesis notation of Lisp does not fit very well with the idea of currying.

Program: Generation of curried and uncurried functions in Scheme.

(define (curry2 f) (lambda(x) (lambda(y) (f x y)))) (define (curry3 f) (lambda(x) (lambda(y) (lambda(z) (f x y z))))) (define (uncurry2 f) (lambda (x y) ((f x) y))) (define (uncurry3 f) (lambda (x y z) (((f x) y) z)))

Exercise 2.18. Playing with curried functions in Scheme

Try out the functions curry2 and curry3 on a number of different functions. You can, for instance, use then curry functions on plus (+) and map. Demonstrate, by a practical example, that the uncurry functions and the curry functions are inverse to each other.

More Exercises Slide Annotated slide Contents Index References

Exercise 2.25. Generation of functions with a very flexible signature

Write a function grouping-abstraction-by-predicates (define (grouping-abstraction-by-predicates collector pred1 pred2) ....) with the following characteristics: It takes 3 parameters. collector is another function of three parameters: (1) The list of those that satisfy pred1, (2) the list of those that satisfy pred2, and (3) the list of all others. pred1 is a predicate pred2 is another predicate grouping-abstraction-by-predicates returns a function that accept an arbitrary number of parameters. The returned function traverses the (list of) parameters passed to it. The elements that satisfy pred1 are collected in one list; The elements that satisfy pred2 are collected in another list; The remaining elements are collected in a third list. The three lists of collected elements are passed to collector. grouping-abstraction-by-predicates returns the result the call to collector. Use grouping-abstraction-by-predicates to generate a function that accepts an arbitrary number of parameter. The functions should add all numbers in the parameter list, form a string of all characters in the parameter list, and throw away all others away. Thus, the generated function should return a list of one number and one string. Here is an example: > (define h (grouping-abstraction-by-predicates (lambda (l1 l2 l3) (list (sum l1) (apply string l2))) number? char?)) > (h 1 3 #\a 4 7 #\b 8 #\c #t 5 #t #t #\d) (28 "abcd") You may want to play with your function for other purposes, with other predicates, etc.

Exercise 2.25. Generalization of curry-2 and curry-3

On an earlier slide page we have seen how to generate curried functions with 2 and 3 parameters - curry2 and curry3. We have also seen how to generate uncurried functions from curried functions - uncurry2 and uncurry3. Now generalize curry2 and curry3: (define (curry f n) ...) where f is a function with n parameters. Similary, generalize uncurry2 and uncurry3: (define (uncurry cf n) ...) where cf is a curried function with n levels. Test your functions appropriately, and be sure that (uncurry (curry f n) n) is equivalent with f (where f is a function of n parameters).

Exercise 2.25. Generalized compose

We have seen the compose function on a previous slide. Let us here work with a variant of compose called self-compose: (define (self-compose-2 f) (lambda (x) (f (f x)))) You first job is to generalize self-compose-2 to self-compose*, which composes the f with itself n times: (define (self-compose* f n) ...) Test your function appropriately. Also, program a function compose* which takes a list of functions as arguments. Each function in the list must be of a single parameter. Your function must return the composition of all the functions. Here is an example of the intended use of the function: > ((compose* (list incr - fac)) 5) -119 fac is here supposed to be the factorial function, and incr is the usual increment function. The expression (compose* (list incr - fac)) should be equivalent to (lambda (x) (incr (- (fac x)))). Are you able to program compose* with a reduction function and compose?

Exercise 2.25. Generation of approximations to differentiated functions

Given a function fr from real numbers to real numbers. Program a higher-order function derivative, which differentiates a function like fr. In this exercise you are asked to work numerically, in order to approximate the function. This stands as a contrast to symbolic differentiation. As examples, (derivative (lambda (x) (* x x))) should behave (almost) as (lambda (x) (* 2 x)); (derivate sin) should behave almost as cos; and (derivate exp) should behave almost like exp itself. Write a function compare-2-functions (compare-2-functions f1 f2 numerical-input-list) which applies f1 and f2 on elements in numerical-input-list, and outputs a list of differences between f1(x) and f2(x) for x in numerical-input-list. Use compare-2-functions to compare (derivative f) and f'. The inspiration to the exercise comes from Christian Wagenknecht's book 'Programmierparadigmen', from Springer Verlag.

Exercise 2.25. The cartesian product of two sets

Program a function that returns the cartesian product of two sets. Each set should be represented as a list. In this exercise, make as much use of map as possible. You may also use a reduction function, if needed. All the involved iteration over lists should done by mapping or reducing functions. (Do not write your own recursive function that 'just does the job').

Exercise 2.25. Powerset

Program a function powerset, which as input takes a set S (represented as a list). The function must return all possible subsets of S. Hint: What is (powerset '())? It should, of course, be a set of sets. Each set is a represented as a list.

Exercise 2.25. Generation of get-prop

In an earlier exercise we programmed an accessor function, get-prop, on property lists. We encountered the following challenges: We would like to have variants of get-prop for different key comparison functions, without programming a number of (almost identical) variants, with copy paste programming. We would like to be able to control the "non-found" value, which normally is boolean false (#f). Boolean false is problematic if the values in the properlist are of type boolean. Write a function (configure-get-prop comparison-function not-found-value) which returns a get-prop function which uses comparison-function (instead of equal?), which returns not-found-value instead of #f. Generate the get-prop function from the earlier exercise, and generate new variants. Play with your generated functions, and make sure that they work as intended.

Chapter 2: Recursion and Higher-order Functions
Course home     Author home     About producing this web     Previous lecture (top)     Next lecture (top)     Previous lecture (bund)     Next lecture (bund)     
Generated: September 17, 2021, 14:11:24