Kurt Nørmark
Institut for Datalogi, Aalborg Universitet

Sammendrag Forrige lektion Næste lektion Stikord Referencer Indhold

Emnet for denne lektion er rekursion.

Begrebet rekursion: Rekursiv problemløsning involverer løsning af delproblemer af samme slags som det overordnede problem

Rekursive strukturer I en rekursiv struktur kan man genfinde helheden i detaljen I datalogiske sammenhænge arbejder vi ofte med rekursive datastrukturer Rekursive processer Rekursive strukturer processeres naturligt rekursivt Nogle rekursive processer afhænger ikke af rekursive strukturer Rekursive processer programmeres med rekursive procedurer eller funktioner

Henvisning Vores første behandling af rekursion

Hverdagsrekursion (1) Slide Indhold Stikord Referencer

Man kan opnå et rekursivt billede hvis et spejl spejler sig et i et andet spejl Tilsvarende rekursive billeder kan frembringes hvis et kamera filmer et TV, som viser signalet fra kameraet

Figur. Et billede af en del af en computerskærm, optaget med et web kamera, hvis billede samtidigt vises på skærmen. Det rekursive billede opstår fordi vinduet på skærmen filmes af kameraet, som viser det optagede billede som en del af vinduet, som hermed påvirker hvad kameraet filmer, som hermed påvirker billedet, osv. Efter nogle få niveuaer fortoner effekten sig i et meget forvrænget billede.

Hverdagsrekursion (2) Slide Indhold Stikord Referencer

Det er muligt - men næppe naturligt for os alle - at opfatte en trappe som en rekursiv struktur

Figur. En trappe opfattet som en rekursiv struktur.

En trappe - opfattet som en rekursiv struktur: En trappe kan være 'tom' - flad gulv En trappe kan bestå af et trin og en tilstødende trappe Processen at gå op ad en trappe: Hvis der er et trin så gå op ad trinnet; Gå dernæst rekursivt op ad resten af trappen. Ellers: Gå et trin fremad på flad gulv.

Program: To trappegangsfunktioner - iterativ og rekursivt - et pseudoprogram.

#include <stdio.h> void walk_stairs_1(staircase s){ for(step = 1, step <= last_step(s); ++step) do_step(step); } void walk_stairs_2(staircase s){ if(!empty_staircase(s)){ do_step(first_step(s)); walk_stairs(remaining_steps(s)) } } int main(void) { /* ... */ return 0; }

Henvisning Tilsvarende eksempel: Lister

Rekursive datastrukturer: Lineære lister Slide Indhold Stikord Referencer

Lineære lister er klassiske eksempler på rekursive datastrukturer

En lineær liste: Enten tom Eller et element (hoved) efterfulgt af en lineær liste (hale)

Figur. En rekursiv lineær liste

Rekursive datastrukturer: Binære træer Slide Indhold Stikord Referencer

Binære træer er et andet klassisk eksempel på rekursive datastrukturer

Et binært træ: Enten tom Eller en knude forbundet med to strukturer, der begge er træer

Figur. Et rekursivt binært træ

Vi viser her en rekursiv funktion, hvor der sker noget både før og efter det rekursive kald.

Program: Læsning på vej op ad bakken/stakken - Skrivning på vej ned.

#include <stdio.h> void f(int i){ char ch; if (i >= 1){ printf("(%1d)Enter a character: ", i); /* Prompt for a char */ scanf(" %c", &ch); f(i-1); /* Recursive call */ printf("(%1d)We read: '%c'\n", i, ch); /* Print the char */ } else printf("(%1d)No more recursive calls\n", i); } int main(void) { f(4); return 0; }

Program: Input til og output fra programmet.

(4)Enter a character: a (3)Enter a character: b (2)Enter a character: c (1)Enter a character: d (0)No more recursive calls (1)We read: 'd' (2)We read: 'c' (3)We read: 'b' (4)We read: 'a'

Billedserie: En illustration af den rekursive udvikling af kaldet f(4).

En illustration af den rekursive udvikling af kaldet f(4).

Billed nr. 1. Kaldet f(4). Brugeren promptes for et tegn. Lad os antage at brugeren taster 'a'. På den vandrette akse forløber tiden.

 

Billed nr. 2. Kaldet f(3). Brugeren promptes igen for et tegn, og der tastes denne gang et 'b'.

 

Billed nr. 3. Kaldet f(2). Brugeren promptes igen for et tegn, og der tastes denne gang et 'c'.

 

Billed nr. 4. Kaldet f(1). Brugeren promptes sidste gang for et tegn, og der tastes denne gang et 'd'.

 

Billed nr. 5. Kaldet f(0). For i lig med 0 udføres else-delen, som vil udskrive 'No more recursive calls'.

 

Billed nr. 6. På vej ned ad stakken udføres det afsluttende printf i if-delen. Her udskrives 'd'.

 

Billed nr. 7. Her udskrives 'c'

 

Billed nr. 8. Og her udskrives 'b'

 

Billed nr. 9. Slutteligt udskrives 'a'. Bemærk disciplinen 'first in, last out' som er typisk for en stak.

 

Funktioner der søger i et array Slide Indhold Stikord Referencer

Vi viser eksempler på iterative og rekursive søgninger i et simpelt array

Program: Lineær søgning i et int array - iterativt programmeret.

#include <stdio.h> /* Find pointer to si in array between fp and tp. Return NULL if not found */ int* find_in_array_1(int si, int *fp, int *tp){ int *pi = fp; while (fp <= tp && *fp != si) ++fp; return *fp == si ? fp : NULL; } int main(void) { int tab[] = {4, 8, -9, 2, 9, 11, 19}; int done = 0, i, *result; while (!done){ printf("Search for: "); scanf(" %d", &i); result = find_in_array_1(i, &tab[0], &tab[0] + 6); if (result) printf("Found\n"); else printf("NOT found\n"); done = i == 0; } return 0; }

Program: Lineær søgning i et int array - rekursivt programmeret.

#include <stdio.h> /* Find pointer to si in array between fp and tp. Return NULL if not found */ int* find_in_array_2(int si, int *fp, int *tp){ if (fp > tp) return NULL; else if (*fp == si) return fp; else return find_in_array_2(si, fp+1, tp); } int main(void) { int tab[] = {4, 8, -9, 2, 9, 11, 19}; int done = 0, i; int *result; while (!done){ printf("Search for: "); scanf(" %d", &i); result = find_in_array_2(i, &tab[0], &tab[0] + 6); if (result) printf("Found\n"); else printf("NOT found\n"); done = i == 0; } return 0; }

Program: Binær søgning i et sorteret int array - rekursivt programmeret.

#include <stdio.h> int* find_in_sorted_array(int si, int *fp, int *tp){ int *mp = fp + (tp - fp)/2; printf("Dist: %d. [%d - %d]\n", (tp - fp), *fp, *tp); if (si == *mp) return mp; else if (fp >= tp) return NULL; else if (si > *mp) return find_in_sorted_array(si, mp+1, tp); /* search in upper part */ else return find_in_sorted_array(si, fp, mp-1); /* search in lower part */ } int main(void) { int tab[] = {-9, 4, 8, 9, 12, 19, 21, 29}; int done = 0, i; int *result; while (!done){ printf("Search for: "); scanf(" %d", &i); result = find_in_sorted_array(i, &tab[0], &tab[0] + 7); if (result) printf("Found\n"); else printf("NOT found\n"); done = i == 0; } return 0; }

Fakultetsfunktionen - et eksempel fra en tidligere lektion Slide Indhold Stikord Referencer

Vi har i tidligere lektioner mødt flere eksempler på rekursive funktioner

Program: Et program med en rekursivt defineret fakultetsfunktion.

#include <stdio.h> unsigned long int factorial(unsigned int n){ if (n == 0) return 1; else return n * factorial(n - 1); } int main(void) { unsigned int k; // Upper limits of k: 12 (if long is 4 bytes) // Upper limits of k: 20 (if long is 8 bytes) for (k = 0; k <= 12; k++) printf("%-20lu %20lu\n", k, factorial(k)); return 0; }

Program: Et tilsvarende program med en iterativ fakultetsfunktion.

#include <stdio.h> unsigned long int factorial(unsigned int n){ unsigned int i; unsigned long result = 1; for(i = 1; i <= n; i++) result *= i; return result; } int main(void) { unsigned int k; for (k = 0; k <= 12; k++) printf("%-20lu %20lu\n", k, factorial(k)); return 0; }

Program: Output fra ovenstående programmer.

0 1 1 1 2 2 3 6 4 24 5 120 6 720 7 5040 8 40320 9 362880 10 3628800 11 39916800 12 479001600

Program: En variation af den rekursive fakultetsfunktionen - ala iteration nu med halerekursion.

#include <stdio.h> // Prototype unsigned long int iterative_factorial(unsigned int n, unsigned int i, unsigned long int result); unsigned long int factorial(unsigned int n){ return iterative_factorial(n, 1, 1); } unsigned long int iterative_factorial(unsigned int n, unsigned int i, unsigned long int result){ if (i <= n) return iterative_factorial(n, i + 1, result * i); else return result; } int main(void) { unsigned int k; // Upper limits of k: 12 (long is 4 bytes) // Upper limits of k: 20 (long is 8 bytes) for (k = 0; k <= 12; k++) printf("%-20lu %20lu\n", k, factorial(k)); return 0; }

Program: Den rekursive og den halerekursive fakultetsfunktion - side om side.

#include <stdio.h> // Prototype unsigned long int it_fac(unsigned int n, unsigned int i, unsigned long int result); unsigned long int factorial(unsigned int n){ return it_fac(n, 1, 1); } unsigned long int it_fac(unsigned int n, unsigned int i, unsigned long int result){ if (i <= n) return it_fac(n, i + 1, result * i); else return result; } unsigned long int fac(unsigned int n){ if (n == 0) return 1; else return n * fac(n - 1); } int main(void) { unsigned int k; // Upper limits of k: 12 (long is 4 bytes) // Upper limits of k: 20 (long is 8 bytes) for (k = 0; k <= 12; k++){ printf("%-20lu %20lu\n", k, factorial(k)); printf("%-20lu %20lu\n", k, fac(k)); } return 0; }

Videoen går ind i flere detaljer om de to varianter af factorial

Fibonacci tal (1) Slide Indhold Stikord Referencer

Serien af Fibonacci tal er en klassisk talrække, i hvilken hvert tal er summen af de to foregående tal

Program: Funktionen fib der udregner det n'te Fibonaccital.

/* Precondition: n >= 0 */ long fib(int n){ long result; if (n == 0) result = 0; else if (n == 1) result = 1; else result = fib(n-1) + fib(n-2); return result; }

Program: Hele programmet.

#include <stdio.h> /* Precondition: n >= 0 */ long fib(int n){ long result; if (n == 0) result = 0; else if (n == 1) result = 1; else result = fib(n-1) + fib(n-2); return result; } int main(void) { int i; for(i = 0; i < 100; i++) printf("Fib(%i) = %li\n", i, fib(i)); return 0; }

Program: Output fra programmet.

Fib(0) = 0 Fib(1) = 1 Fib(2) = 1 Fib(3) = 2 Fib(4) = 3 Fib(5) = 5 Fib(6) = 8 Fib(7) = 13 Fib(8) = 21 Fib(9) = 34 Fib(10) = 55 Fib(11) = 89 Fib(12) = 144 Fib(13) = 233 Fib(14) = 377 Fib(15) = 610 Fib(16) = 987 Fib(17) = 1597 Fib(18) = 2584 Fib(19) = 4181 Fib(20) = 6765 Fib(21) = 10946 Fib(22) = 17711 Fib(23) = 28657 Fib(24) = 46368 Fib(25) = 75025 Fib(26) = 121393 Fib(27) = 196418 Fib(28) = 317811 Fib(29) = 514229 Fib(30) = 832040 Fib(31) = 1346269 Fib(32) = 2178309 Fib(33) = 3524578 Fib(34) = 5702887 Fib(35) = 9227465 Fib(36) = 14930352 Fib(37) = 24157817 Fib(38) = 39088169 Fib(39) = 63245986 ...

Program: En udgave af programmet som holder regnskab med antallet af additioner.

#include <stdio.h> long plus_count = 0; long fib(long n){ long result; if (n == 0) result = 0; else if (n == 1) result = 1; else { result = fib(n-1) + fib(n-2); plus_count++; } return result; } int main(void) { int i; long fib_res; for(i = 0; i < 100; i++){ plus_count = 0; fib_res = fib(i); printf("Fib(%2i) = %-15li %15li\n", i, fib_res, plus_count ); } return 0; }

Program: Output fra programmet, som holder regnskab med antal addtioner.

Fib( 0) = 0 0 Fib( 1) = 1 0 Fib( 2) = 1 1 Fib( 3) = 2 2 Fib( 4) = 3 4 Fib( 5) = 5 7 Fib( 6) = 8 12 Fib( 7) = 13 20 Fib( 8) = 21 33 Fib( 9) = 34 54 Fib(10) = 55 88 Fib(11) = 89 143 Fib(12) = 144 232 Fib(13) = 233 376 Fib(14) = 377 609 Fib(15) = 610 986 Fib(16) = 987 1596 Fib(17) = 1597 2583 Fib(18) = 2584 4180 Fib(19) = 4181 6764 Fib(20) = 6765 10945 Fib(21) = 10946 17710 Fib(22) = 17711 28656 Fib(23) = 28657 46367 Fib(24) = 46368 75024 Fib(25) = 75025 121392 Fib(26) = 121393 196417 Fib(27) = 196418 317810 Fib(28) = 317811 514228 Fib(29) = 514229 832039 Fib(30) = 832040 1346268 Fib(31) = 1346269 2178308 Fib(32) = 2178309 3524577 Fib(33) = 3524578 5702886 Fib(34) = 5702887 9227464 Fib(35) = 9227465 14930351 Fib(36) = 14930352 24157816 Fib(37) = 24157817 39088168 Fib(38) = 39088169 63245985 Fib(39) = 63245986 102334154 ...

Fibonacci tal (2) Slide Indhold Stikord Referencer

Funktionen fib foretager store mængder af unødvendige genberegninger Antallet af additioner vokser eksponentielt i forhold til parameteren n

Figur. En illustration af beregningsprocessen af fib(5)

Mere effektive løsninger: En iterativ rækkeudvikling af Fibonacci tallene. En rekursiv løsning, som kortslutter genberegningerne af Fibonacci tallene.

Fibonacci tal (3) Slide Indhold Stikord Referencer

Vi viser her mere effektive udgaver af fib funktionen

Program: En iterativ udgave af fib programmeret med en for-løkke.

#include <stdio.h> long fib(long n){ long small, large, temp, i; for (small = 0, large = 1, i = 0; i < n; i++){ temp = small; small = large; large = large + temp; } return small; } int main(void) { long i; for(i = 0; i < 100; i++){ printf("Fib(%li) = %li\n", i, fib(i) ); } return 0; }

Program: En iterativ udgave af fib programmeret rekursivt.

#include <stdio.h> // Prototype: long fib_iter(int n, int i, long small, long large); long fib(int n){ return fib_iter(n, 0, 0, 1); } long fib_iter(int n, int i, long small, long large){ // fib(i) == small if (i == n) return small; else return fib_iter(n, i + 1, large, large + small); } int main(void) { long i; for(i = 0; i < 100; i++) printf("Fib(%li) = %li\n", i, fib(i)); return 0; }

Program: Output fra programmerne.

Fib(0) = 0 Fib(1) = 1 Fib(2) = 1 Fib(3) = 2 Fib(4) = 3 Fib(5) = 5 Fib(6) = 8 Fib(7) = 13 Fib(8) = 21 Fib(9) = 34 Fib(10) = 55 Fib(11) = 89 Fib(12) = 144 Fib(13) = 233 Fib(14) = 377 Fib(15) = 610 Fib(16) = 987 Fib(17) = 1597 Fib(18) = 2584 Fib(19) = 4181 Fib(20) = 6765 Fib(21) = 10946 Fib(22) = 17711 Fib(23) = 28657 Fib(24) = 46368 Fib(25) = 75025 Fib(26) = 121393 Fib(27) = 196418 Fib(28) = 317811 Fib(29) = 514229 Fib(30) = 832040 Fib(31) = 1346269 Fib(32) = 2178309 Fib(33) = 3524578 Fib(34) = 5702887 Fib(35) = 9227465 Fib(36) = 14930352 Fib(37) = 24157817 Fib(38) = 39088169 Fib(39) = 63245986 Fib(40) = 102334155 Fib(41) = 165580141 Fib(42) = 267914296 Fib(43) = 433494437 Fib(44) = 701408733 Fib(45) = 1134903170 Fib(46) = 1836311903 Fib(47) = -1323752223 Fib(48) = 512559680 Fib(49) = -811192543 Fib(50) = -298632863 Fib(51) = -1109825406 Fib(52) = -1408458269 Fib(53) = 1776683621 Fib(54) = 368225352 Fib(55) = 2144908973 Fib(56) = -1781832971 Fib(57) = 363076002 Fib(58) = -1418756969 Fib(59) = -1055680967 Fib(60) = 1820529360 Fib(61) = 764848393 Fib(62) = -1709589543 Fib(63) = -944741150 Fib(64) = 1640636603 Fib(65) = 695895453 Fib(66) = -1958435240 Fib(67) = -1262539787 Fib(68) = 1073992269 Fib(69) = -188547518 Fib(70) = 885444751 Fib(71) = 696897233 Fib(72) = 1582341984 Fib(73) = -2015728079 Fib(74) = -433386095 Fib(75) = 1845853122 Fib(76) = 1412467027 Fib(77) = -1036647147 Fib(78) = 375819880 Fib(79) = -660827267 Fib(80) = -285007387 Fib(81) = -945834654 Fib(82) = -1230842041 Fib(83) = 2118290601 Fib(84) = 887448560 Fib(85) = -1289228135 Fib(86) = -401779575 Fib(87) = -1691007710 Fib(88) = -2092787285 Fib(89) = 511172301 Fib(90) = -1581614984 Fib(91) = -1070442683 Fib(92) = 1642909629 Fib(93) = 572466946 Fib(94) = -2079590721 Fib(95) = -1507123775 Fib(96) = 708252800 Fib(97) = -798870975 Fib(98) = -90618175 Fib(99) = -889489150

Program: En memoriseret pseudoprogram af fib.

#include <stdio.h> long fib(long n){ /* working program: fib-memo.c - an exercise*/ long result; Erklaer huskevaerk; if (n == 0) result = 0; else if (n == 1) result = 1; else if (Vi allerede har beregnet vaerdien en gang) result = den huskede vaerdi; else { result = fib(n-1) + fib(n-2); Husk paa vaerdien; } return result; } int main(void) { long i; for(i = 0; i < 100; i++) printf("Fib(%li) = %li\n", i, fib(i)); return 0; }

Opgave 11.3. En Fibonacci funktion med huskeværk

Den rekursive fib funktion, som kan programmeres således long fib(int n){ long result; if (n == 0) result = 0; else if (n == 1) result = 1; else result = fib(n-1) + fib(n-2); return result; } lider af et alvorligt effektivitetsproblem. Hvert kald af fib(n) for n > 1 leder til to andre kald af fib. Mange af disse kald har allerede været udført en eller flere gange tidligere. Prøv f.eks. at danne dig et overblik over hvor mange gange fib(2) bliver kaldt når vi beregner fib(5). Ideen i denne opgave er at huske på (lagre) værdien af fib(n), når den er beregnet første gang. Hvis vi efterfølgende kalder fib(n) igen, trækker vi værdien ud af lageret snarere end at genberegne fib(n) rekursivt. Denne teknik kaldes for memoisering. Her er det pseudoprogram vi har studeret: long fib(long n){ /* working program: fib-memo.c - an exercise*/ long result; Erklaer huskevaerk; if (n == 0) result = 0; else if (n == 1) result = 1; else if (Vi allerede har beregnet vaerdien en gang) result = den huskede vaerdi; else { result = fib(n-1) + fib(n-2); Husk paa vaerdien; } return result; } int main(void) { long i; for(i = 0; i < 100; i++) printf("Fib(%li) = %li\n", i, fib(i)); return 0; } Modificer ovenstående versioner af fib, således at den lagrer værdien af fib(n) når udtrykket er beregnet. Og således at den udtrækker og returnerer en lagret værdi, i stedet for at gå i gang med en genberegning. Det er oplagt at allokere et array af element-typen long int til formålet. Overvej en anvendelse af en statisk lokal variabel! Kald den oprindelige af fib og din nye variant af fib funktionen med alle heltal mellem n og 45, og vurder dermed effekten af memoiseringen.

Opgave 11.3. Palindromer

Et palindrom er en tekststreng, som læses ens både forfra og bagfra. Eksempelvis er strengen "regninger" et palindrom. Vi kan også sige at et palindrom er en tekststreng som er lig med sin egen strengomvending. Skriv først en iterativ funktion int is_palindrome_iter(char *str), der afgør om str er et palindrom. En iterativ funktion er en funktion, som programmeres ved brug af en while-løkke eller en for-løkke. Funktionen skal returnere 1 hvis str er et palindrom, og 0 hvis str ikke er et palindrom. Skriv dernæst en tilsvarende rekursiv udgave int is_palindrome_rec(char *str). Den rekursive funktion skal løse nøjagtig det samme problem som den iterative funktion; Altså om parameteren str er et palindrom. Den skal gøre dette ved at undersøge om en bestemt (lidt mindre) delstreng af strengen er et palindrom. Hvis det hjælper dig, kan du overveje at indføre en hjælpefunktion til is_palindrome_rec, for at gøre dette. Målet med denne opgave er at opnå viden og færdigheder i at arbejde med såvel rekursive som iterativt programmerede funktioner. Målet er endvidere at opnå yderligere viden og færdigheder i simpel programmering med tekststrenge.

Potensopløftning (1) Slide Indhold Stikord Referencer

På denne side viser vi en simpel, rekursiv potensopløftningsfunktion

Beregningsidé: potens > 0:   tal potens = tal potens-1 · tal potens = 0:   tal 0 = 1.0 potens < 0:   1.0 / tal -potens

Program: Den simple power funktion.

double power(double number, int pow){ double result; if (pow == 0) result = 1.0; else if (pow > 0) result = number * power(number, pow - 1); else result = 1.0 / power(number, -pow); return result; } int main(void) { double number; int pow; do{ printf("Enter number and pow in power(number,pow).\n" "0 0 terminates: "); scanf("%lf %i", &number, &pow); printf("power(%f,%i) = %f\n", number, pow, power(number,pow)); }

Potensopløftning (2) Slide Indhold Stikord Referencer

På denne side viser vi en mere effektiv rekursiv potensopløftningsfunktion

Beregningsidé: potens > 0, potens er lige:   tal potens = ( tal potens/2 ) 2 potens > 0, potens er ulige   tal potens = tal potens-1 · tal potens = 0:   tal 0 = 1.0 potens < 0:   1.0 / tal -potens

Program: Den hurtige power funktion.

double power(double number, int pow){ double result; printf("power(%lf,%i)\n", number, pow); // reveals the computation if (pow == 0) result = 1.0; else if (pow > 0 && even(pow)) result = sqr(power(number,pow/2)); else if (pow > 0 && odd(pow)) result = number * power(number, pow - 1); else result = 1.0 / power(number, -pow); return result; }

Program: Den hurtige power funktion, som afslører de rekursive kald.

double power(double number, int pow){ double result; printf("power(%lf,%i)\n", number, pow); // reveals the computation if (pow == 0) result = 1.0; else if (pow > 0 && even(pow)) result = sqr(power(number,pow/2)); else if (pow > 0 && odd(pow)) result = number * power(number, pow - 1); else result = 1.0 / power(number, -pow); return result; }

Billedserie: Illustration af kaldet power(2.0,10), hvor power er den effektive version.

Illustration af kaldet power(2.0,10), hvor power er den effektive version.

Billed nr. 1. Kaldet power(2.0, 10). Result har ikke fået en værdi.

 

Billed nr. 2. Da 10 er lige forårsages det rekursive kald power(2.0 ,5)

 

Billed nr. 3. Da 5 er ulige kaldes power(2.0, 4).

 

Billed nr. 4. For 4 lige kaldes power(2.0, 2)

 

Billed nr. 5. Da 2 er lige kaldes power(2.0 ,1). Bemærk stadig, at ingen af result variablene har fået en værdi

 

Billed nr. 6. Vi når til til kaldet power(2.0, 0) som er basistilfældet i rekursionen.

 

Billed nr. 7. En gentagelse af det tidligere billede, hvor result har fået værdien 1.0 (et specialtilfælde i beregningen).

 

Billed nr. 8. Result bliver her 2.0 * 1.0, altså 2.0, idet pow er ulige.

 

Billed nr. 9. Result er sqr(2.0), altså 4.0, idet pow er lige.

 

Billed nr. 10. Result er sqr(4.0), altså 16.0, idet pow igen er lige.

 

Billed nr. 11. Da pow er ulige på dette niveau bliver result 2.0 * 16.0, altså 32.0

 

Billed nr. 12. Da pow er 10 på dette niveau (altså et lige tal) kvadreres det forrige resultat, altså sqr(32.0), som er 1024.0

 

Potensopløftning (3) Slide Indhold Stikord Referencer

Der er meget stor forskel på antallet af multiplikationer i de to udgaver af potensopløftningsfunktionen Vi illustrerer herunder rekursionens udvikling af den hurtige power funktion Vi skriver også et program som belyser forskellen mellem antallet af udførte multiplikationer

Program: Et program der tæller antallet af multiplikationer i de to potens funktioner.

#include <stdio.h> double sqr(double); int even (int); int odd (int); int mult_no_1, mult_no_2; double power1(double number, int pow){ double result; if (pow == 0) result = 1.0; else if (pow > 0){ result = number * power1(number, pow - 1); mult_no_1++; } else result = 1.0 / power1(number, -pow); return result; } double power2(double number, int pow){ double result; if (pow == 0) result = 1.0; else if (pow > 0 && even(pow)){ result = sqr(power2(number,pow/2)); mult_no_2++; } else if (pow > 0 && odd(pow)){ result = number * power2(number, pow - 1); mult_no_2++; } else result = 1.0 / power2(number, -pow); return result; } int main(void) { int i; double res1, res2; for(i = 1; i < 500; i += 5){ mult_no_1 = 0; mult_no_2 = 0; res1 = power1(1.01,i); res2 = power2(1.01,i); printf("power1(1.01,%i) = %7.5f (%i multiplications)\n" "power2(1.01,%i) = %7.5f (%i multiplications). \n\n", i, res1, mult_no_1, i, res2, mult_no_2); } return 0; } double sqr(double d){ return d*d; } int even (int i){ return i % 2 == 0; } int odd (int i){ return i % 2 != 0; }

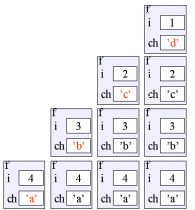
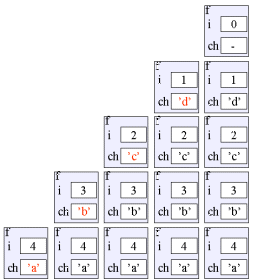
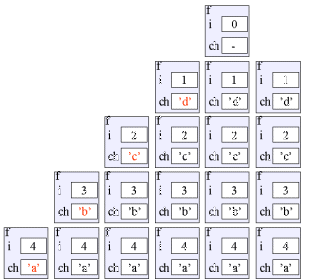
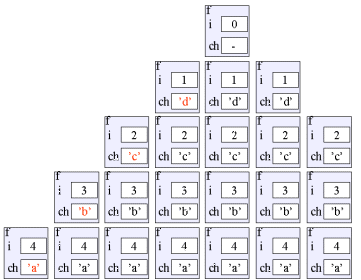
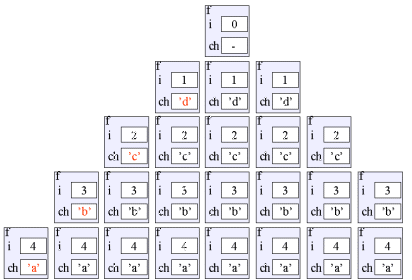
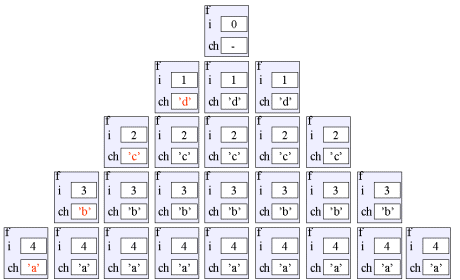
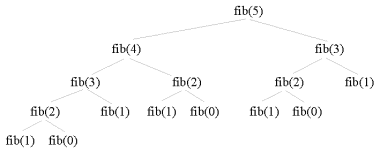
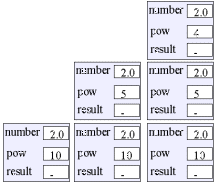
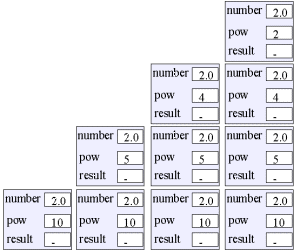
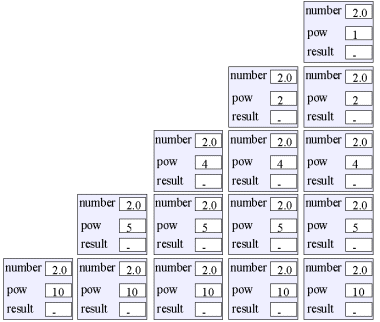
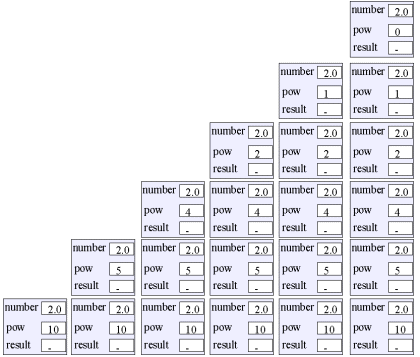
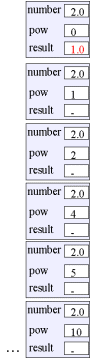
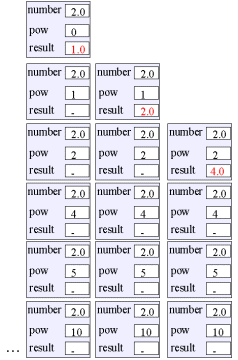
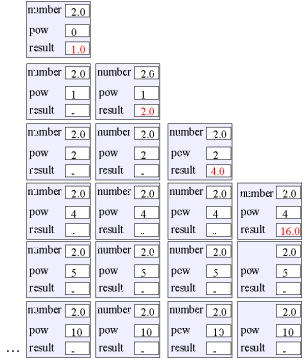
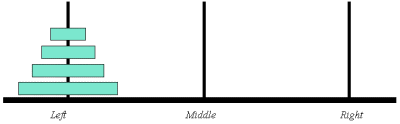
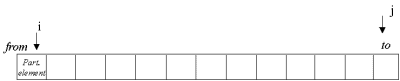
Program: Output fra programmet.

power1(1.01,1) = 1.01000 (1 multiplications) power2(1.01,1) = 1.01000 (1 multiplications). power1(1.01,6) = 1.06152 (6 multiplications) power2(1.01,6) = 1.06152 (4 multiplications). power1(1.01,11) = 1.11567 (11 multiplications) power2(1.01,11) = 1.11567 (6 multiplications). power1(1.01,16) = 1.17258 (16 multiplications) power2(1.01,16) = 1.17258 (5 multiplications). power1(1.01,21) = 1.23239 (21 multiplications) power2(1.01,21) = 1.23239 (7 multiplications). power1(1.01,26) = 1.29526 (26 multiplications) power2(1.01,26) = 1.29526 (7 multiplications). power1(1.01,31) = 1.36133 (31 multiplications) power2(1.01,31) = 1.36133 (9 multiplications). power1(1.01,36) = 1.43077 (36 multiplications) power2(1.01,36) = 1.43077 (7 multiplications). power1(1.01,41) = 1.50375 (41 multiplications) power2(1.01,41) = 1.50375 (8 multiplications). power1(1.01,46) = 1.58046 (46 multiplications) power2(1.01,46) = 1.58046 (9 multiplications). power1(1.01,51) = 1.66108 (51 multiplications) power2(1.01,51) = 1.66108 (9 multiplications). power1(1.01,56) = 1.74581 (56 multiplications) power2(1.01,56) = 1.74581 (8 multiplications). power1(1.01,61) = 1.83486 (61 multiplications) power2(1.01,61) = 1.83486 (10 multiplications). power1(1.01,66) = 1.92846 (66 multiplications) power2(1.01,66) = 1.92846 (8 multiplications). power1(1.01,71) = 2.02683 (71 multiplications) power2(1.01,71) = 2.02683 (10 multiplications). power1(1.01,76) = 2.13022 (76 multiplications) power2(1.01,76) = 2.13022 (9 multiplications). power1(1.01,81) = 2.23888 (81 multiplications) power2(1.01,81) = 2.23888 (9 multiplications). power1(1.01,86) = 2.35309 (86 multiplications) power2(1.01,86) = 2.35309 (10 multiplications). power1(1.01,91) = 2.47312 (91 multiplications) power2(1.01,91) = 2.47312 (11 multiplications). power1(1.01,96) = 2.59927 (96 multiplications) power2(1.01,96) = 2.59927 (8 multiplications). power1(1.01,101) = 2.73186 (101 multiplications) power2(1.01,101) = 2.73186 (10 multiplications). power1(1.01,106) = 2.87121 (106 multiplications) power2(1.01,106) = 2.87121 (10 multiplications). power1(1.01,111) = 3.01768 (111 multiplications) power2(1.01,111) = 3.01768 (12 multiplications). power1(1.01,116) = 3.17161 (116 multiplications) power2(1.01,116) = 3.17161 (10 multiplications). power1(1.01,121) = 3.33339 (121 multiplications) power2(1.01,121) = 3.33339 (11 multiplications). power1(1.01,126) = 3.50343 (126 multiplications) power2(1.01,126) = 3.50343 (12 multiplications). power1(1.01,131) = 3.68214 (131 multiplications) power2(1.01,131) = 3.68214 (10 multiplications). power1(1.01,136) = 3.86996 (136 multiplications) power2(1.01,136) = 3.86996 (9 multiplications). power1(1.01,141) = 4.06737 (141 multiplications) power2(1.01,141) = 4.06737 (11 multiplications). power1(1.01,146) = 4.27485 (146 multiplications) power2(1.01,146) = 4.27485 (10 multiplications). power1(1.01,151) = 4.49291 (151 multiplications) power2(1.01,151) = 4.49291 (12 multiplications). power1(1.01,156) = 4.72209 (156 multiplications) power2(1.01,156) = 4.72209 (11 multiplications). power1(1.01,161) = 4.96296 (161 multiplications) power2(1.01,161) = 4.96296 (10 multiplications). power1(1.01,166) = 5.21613 (166 multiplications) power2(1.01,166) = 5.21613 (11 multiplications). power1(1.01,171) = 5.48220 (171 multiplications) power2(1.01,171) = 5.48220 (12 multiplications). power1(1.01,176) = 5.76185 (176 multiplications) power2(1.01,176) = 5.76185 (10 multiplications). power1(1.01,181) = 6.05576 (181 multiplications) power2(1.01,181) = 6.05576 (12 multiplications). power1(1.01,186) = 6.36466 (186 multiplications) power2(1.01,186) = 6.36466 (12 multiplications). power1(1.01,191) = 6.68933 (191 multiplications) power2(1.01,191) = 6.68933 (14 multiplications). power1(1.01,196) = 7.03055 (196 multiplications) power2(1.01,196) = 7.03055 (10 multiplications). power1(1.01,201) = 7.38918 (201 multiplications) power2(1.01,201) = 7.38918 (11 multiplications). power1(1.01,206) = 7.76610 (206 multiplications) power2(1.01,206) = 7.76610 (12 multiplications). power1(1.01,211) = 8.16225 (211 multiplications) power2(1.01,211) = 8.16225 (12 multiplications). power1(1.01,216) = 8.57861 (216 multiplications) power2(1.01,216) = 8.57861 (11 multiplications). power1(1.01,221) = 9.01620 (221 multiplications) power2(1.01,221) = 9.01620 (13 multiplications). power1(1.01,226) = 9.47612 (226 multiplications) power2(1.01,226) = 9.47612 (11 multiplications). power1(1.01,231) = 9.95950 (231 multiplications) power2(1.01,231) = 9.95950 (13 multiplications). power1(1.01,236) = 10.46753 (236 multiplications) power2(1.01,236) = 10.46753 (12 multiplications). power1(1.01,241) = 11.00148 (241 multiplications) power2(1.01,241) = 11.00148 (12 multiplications). power1(1.01,246) = 11.56267 (246 multiplications) power2(1.01,246) = 11.56267 (13 multiplications). power1(1.01,251) = 12.15248 (251 multiplications) power2(1.01,251) = 12.15248 (14 multiplications). power1(1.01,256) = 12.77238 (256 multiplications) power2(1.01,256) = 12.77238 (9 multiplications). power1(1.01,261) = 13.42390 (261 multiplications) power2(1.01,261) = 13.42390 (11 multiplications). power1(1.01,266) = 14.10865 (266 multiplications) power2(1.01,266) = 14.10865 (11 multiplications). power1(1.01,271) = 14.82833 (271 multiplications) power2(1.01,271) = 14.82833 (13 multiplications). power1(1.01,276) = 15.58473 (276 multiplications) power2(1.01,276) = 15.58473 (11 multiplications). power1(1.01,281) = 16.37970 (281 multiplications) power2(1.01,281) = 16.37970 (12 multiplications). power1(1.01,286) = 17.21523 (286 multiplications) power2(1.01,286) = 17.21523 (13 multiplications). power1(1.01,291) = 18.09338 (291 multiplications) power2(1.01,291) = 18.09338 (12 multiplications). power1(1.01,296) = 19.01633 (296 multiplications) power2(1.01,296) = 19.01633 (11 multiplications). power1(1.01,301) = 19.98635 (301 multiplications) power2(1.01,301) = 19.98635 (13 multiplications). power1(1.01,306) = 21.00586 (306 multiplications) power2(1.01,306) = 21.00586 (12 multiplications). power1(1.01,311) = 22.07737 (311 multiplications) power2(1.01,311) = 22.07737 (14 multiplications). power1(1.01,316) = 23.20353 (316 multiplications) power2(1.01,316) = 23.20353 (13 multiplications). power1(1.01,321) = 24.38715 (321 multiplications) power2(1.01,321) = 24.38715 (11 multiplications). power1(1.01,326) = 25.63114 (326 multiplications) power2(1.01,326) = 25.63114 (12 multiplications). power1(1.01,331) = 26.93858 (331 multiplications) power2(1.01,331) = 26.93858 (13 multiplications). power1(1.01,336) = 28.31272 (336 multiplications) power2(1.01,336) = 28.31272 (11 multiplications). power1(1.01,341) = 29.75695 (341 multiplications) power2(1.01,341) = 29.75695 (13 multiplications). power1(1.01,346) = 31.27486 (346 multiplications) power2(1.01,346) = 31.27486 (13 multiplications). power1(1.01,351) = 32.87019 (351 multiplications) power2(1.01,351) = 32.87019 (15 multiplications). power1(1.01,356) = 34.54690 (356 multiplications) power2(1.01,356) = 34.54690 (12 multiplications). power1(1.01,361) = 36.30914 (361 multiplications) power2(1.01,361) = 36.30914 (13 multiplications). power1(1.01,366) = 38.16127 (366 multiplications) power2(1.01,366) = 38.16127 (14 multiplications). power1(1.01,371) = 40.10788 (371 multiplications) power2(1.01,371) = 40.10788 (14 multiplications). power1(1.01,376) = 42.15378 (376 multiplications) power2(1.01,376) = 42.15378 (13 multiplications). power1(1.01,381) = 44.30405 (381 multiplications) power2(1.01,381) = 44.30405 (15 multiplications). power1(1.01,386) = 46.56400 (386 multiplications) power2(1.01,386) = 46.56400 (11 multiplications). power1(1.01,391) = 48.93923 (391 multiplications) power2(1.01,391) = 48.93923 (13 multiplications). power1(1.01,396) = 51.43562 (396 multiplications) power2(1.01,396) = 51.43562 (12 multiplications). power1(1.01,401) = 54.05936 (401 multiplications) power2(1.01,401) = 54.05936 (12 multiplications). power1(1.01,406) = 56.81693 (406 multiplications) power2(1.01,406) = 56.81693 (13 multiplications). power1(1.01,411) = 59.71516 (411 multiplications) power2(1.01,411) = 59.71516 (14 multiplications). power1(1.01,416) = 62.76124 (416 multiplications) power2(1.01,416) = 62.76124 (11 multiplications). power1(1.01,421) = 65.96269 (421 multiplications) power2(1.01,421) = 65.96269 (13 multiplications). power1(1.01,426) = 69.32745 (426 multiplications) power2(1.01,426) = 69.32745 (13 multiplications). power1(1.01,431) = 72.86385 (431 multiplications) power2(1.01,431) = 72.86385 (15 multiplications). power1(1.01,436) = 76.58064 (436 multiplications) power2(1.01,436) = 76.58064 (13 multiplications). power1(1.01,441) = 80.48702 (441 multiplications) power2(1.01,441) = 80.48702 (14 multiplications). power1(1.01,446) = 84.59266 (446 multiplications) power2(1.01,446) = 84.59266 (15 multiplications). power1(1.01,451) = 88.90774 (451 multiplications) power2(1.01,451) = 88.90774 (13 multiplications). power1(1.01,456) = 93.44293 (456 multiplications) power2(1.01,456) = 93.44293 (12 multiplications). power1(1.01,461) = 98.20946 (461 multiplications) power2(1.01,461) = 98.20946 (14 multiplications). power1(1.01,466) = 103.21913 (466 multiplications) power2(1.01,466) = 103.21913 (13 multiplications). power1(1.01,471) = 108.48434 (471 multiplications) power2(1.01,471) = 108.48434 (15 multiplications). power1(1.01,476) = 114.01813 (476 multiplications) power2(1.01,476) = 114.01813 (14 multiplications). power1(1.01,481) = 119.83420 (481 multiplications) power2(1.01,481) = 119.83420 (13 multiplications). power1(1.01,486) = 125.94695 (486 multiplications) power2(1.01,486) = 125.94695 (14 multiplications). power1(1.01,491) = 132.37151 (491 multiplications) power2(1.01,491) = 132.37151 (15 multiplications). power1(1.01,496) = 139.12379 (496 multiplications) power2(1.01,496) = 139.12379 (13 multiplications).

Opgave 11.4. Heltalsdivision og restuddragning med rekursive funktioner

Programmer en funktion int quotient(int dividend, int divisor) som beregner dividend / divisor ved brug af rekursion (ved gentagen subtraktion). Skriv ligeledes en rekursiv funktion int modulus(int dividend, int divisor) som beregner resten, dividend % divisor.

Towers of Hanoi er en gammel asiatisk overlevering om munke, der skulle flytte 64 skiver fra én søjle til en anden Ifølge legenden ville templet og verden gå til grunde inden arbejdet kunne fuldføres En skive ad gangen - aldrig en stor skive oven på en lille

Figur. En illustration af Towers of Hanoi med fire skiver.

Towers of Hanoi (2) Slide Indhold Stikord Referencer

Problemet: Flyt stakken af skiver fra venstre stang til højre stang med brug af midterste stang som 'mellemstation' Skiverne skal flyttes én ad gangen En større skive må aldrig placeres oven på en mindre skive

Henvisning Del og hersk

Løsningen på næste side er en rekursiv del og hersk løsning

Towers of Hanoi (3) Slide Indhold Stikord Referencer

Vi programmerer en løsning på problemet som kun viser hvilke flytninger der skal foretages.

Program: Den centrale funktion i "Towers of Hanoi".

/* Move n discs from tower a to tower b via tower c */ void hanoi(int n, tower a, tower b, tower c){ if (n == 1) move_one_disc(a,b); else { hanoi(n-1,a,c,b); move_one_disc(a,b); hanoi(n-1,c,b,a); } }

Program: Hele programmet.

#include <stdio.h> enum tower {left, middle, right}; typedef enum tower tower; void move_one_disc(tower a, tower b); char *tower_out(tower t); /* Move n discs from tower a to tower b via tower c */ void hanoi(int n, tower a, tower b, tower c){ if (n == 1) move_one_disc(a,b); else { hanoi(n-1,a,c,b); move_one_disc(a,b); hanoi(n-1,c,b,a); } } void move_one_disc(tower a, tower b){ static long count = 0; count++; printf("%5i. Move disc from %6s tower to %6s tower\n", count, tower_out(a), tower_out(b)); } char *tower_out(tower t){ static char *result; switch (t){ case left: result = "LEFT"; break; case middle: result = "MIDDLE"; break; case right: result = "RIGHT"; break; } return result; } int main(void) { int number_of_discs; printf("Move how many discs (form LEFT to RIGHT via MIDDLE): "); scanf("%d", &number_of_discs); hanoi(number_of_discs, left, right, middle); return 0; }

Program: Output fra programmet ved flytning af fire skiver - fra LEFT til RIGHT via MIDDLE.

1. Move disc from LEFT tower to MIDDLE tower 2. Move disc from LEFT tower to RIGHT tower 3. Move disc from MIDDLE tower to RIGHT tower 4. Move disc from LEFT tower to MIDDLE tower 5. Move disc from RIGHT tower to LEFT tower 6. Move disc from RIGHT tower to MIDDLE tower 7. Move disc from LEFT tower to MIDDLE tower 8. Move disc from LEFT tower to RIGHT tower 9. Move disc from MIDDLE tower to RIGHT tower 10. Move disc from MIDDLE tower to LEFT tower 11. Move disc from RIGHT tower to LEFT tower 12. Move disc from MIDDLE tower to RIGHT tower 13. Move disc from LEFT tower to MIDDLE tower 14. Move disc from LEFT tower to RIGHT tower 15. Move disc from MIDDLE tower to RIGHT tower

Towers of Hanoi (4) Slide Indhold Stikord Referencer

Det er let at se at antallet af flytninger F(n) vokser eksponentielt med antallet af diske i tårnet. Mere præcist ser vi at F(n) = 2 n - 1.

Tabel. En table der viser antallet af flytninger og køretider af hanoi funktionen. Køretiderne i tredje kolonne er angivet under antagelsen af vi kan flytte 109 skiver pr. sekund. Køretiderne i fjerde kolonne er angivet under antagelsen af vi kan flytte 103 skiver pr. sekund.

n 2n 10-9 · 2n 10-3 · 2n 5 32 3.2 · 10-8 sek 3.2 · 10-2 sek 25 3.4 · 107 0.03 sek 9.3 timer 50 1.1 · 1015 13 dage 35702 år 65 3.7 · 1019 1170 år 1.17 · 109 år 80 1.2 · 1024 3.8 · 107 år 3.8 · 1013 år 100 1.2 · 1039 4.0 · 1013 år 4.0 · 1020 år

Quicksort er et eksempel på en rekursiv sorteringsteknik der typisk er meget mere effektiv end f.eks. boblesortering

Algoritmisk idé: Udvælg et vilkårligt deleelement blandt tabellens elementer Reorganiser tabellen således at den består af to dele: En venstre del hvor alle elementer er mindre end eller lig med deleelementet En højre del hvor alle elementer er større end eller lig med deleelementet Sorter både venstre og højre del af tabellen rekursivt, efter samme idé som netop beskrevet

Henvisning Boblesortering

Quicksort er et andet eksempel på en rekursiv del og hersk løsning En stor del af arbejdet består i opdelning af problemet i to mindre delproblemer, som egner sig til en rekursiv løsning Sammensætningen af delproblemernes løsninger er helt triviel

Quicksort (2) Slide Indhold Stikord Referencer

Vi viser først den overordnede quicksort funktion Den viste udgave sorterer blot heltal

Program: Den rekursive quicksort funktion.

/* Sort the array interval a[from..to] */ void quicksort(element a[], index from, index to){ index point1, point2; if (from < to){ do_partitioning(a, from, to, &point1, &point2); partitioning_info(a, from, to, point1, point2); quicksort(a, from, point1); quicksort(a, point2, to); } }

Quicksort (3) Slide Indhold Stikord Referencer

Den centrale del af quicksort er funktionen do_partitioning

Program: Funktionen do_partitioning der deler tabellens elementer op i store og små.

/* Do a partitioning of a, and return the partitioning points in *point_left and *point_right */ void do_partitioning(element a[], index from, index to, index *point_left, index *point_right){ index i,j; element partitioning_el; i = from - 1; j = to + 1; partitioning_el = a[from]; do{ do {i++;} while (a[i] < partitioning_el); do {j--;} while (a[j] > partitioning_el); if (i < j) swap(&a[i],&a[j]); } while (i < j); if (i > j) { *point_left = j; *point_right = i;} else { *point_left = j-1; *point_right = i+1;} }

Program: Hele programmet.

#include <stdio.h> typedef int index; typedef int element; void do_partitioning(element[], index, index, index*, index*); void swap(index*, index*); void prn_array(char* s, int a[], int from, int to); void partitioning_info(element a[], index from, index to, index point_left, index point_right); /* Sort the array interval a[from..to] */ void quicksort(element a[], index from, index to){ index point1, point2; if (from < to){ do_partitioning(a, from, to, &point1, &point2); partitioning_info(a, from, to, point1, point2); quicksort(a, from, point1); quicksort(a, point2, to); } } void partitioning_info(element a[], index from, index to, index point_left, index point_right){ printf("Partitioning a[%i .. %i]\n", from, to); prn_array("Small:", a, from, point_left); printf("\n"); prn_array("Large:", a, point_left+1, to); printf("\n\n"); } /* Do a partitioning of a, and return the partitioning points in *point_left and *point_right */ void do_partitioning(element a[], index from, index to, index *point_left, index *point_right){ index i,j; element partitioning_el; i = from - 1; j = to + 1; partitioning_el = a[from]; do{ do {i++;} while (a[i] < partitioning_el); do {j--;} while (a[j] > partitioning_el); if (i < j) swap(&a[i],&a[j]); } while (i < j); if (i > j) { *point_left = j; *point_right = i;} else { *point_left = j-1; *point_right = i+1;} } int main(void) { int a[] = {7, 3, 66, 3, -5, 22, -77, 2}; int n; n = sizeof(a) / sizeof(int); prn_array("Before", a, 0, n-1); printf("\n\n"); quicksort(a, 0, n-1); prn_array(" After", a, 0, n-1); printf("\n\n"); putchar('\n'); return 0; } void swap(element *p, element *q) { element tmp; tmp = *p; *p = *q; *q = tmp; } void prn_array(char* s , int a[], int from, int to) { int i; printf("%s a[%i,%i]: ", s, from, to); for (i = from; i <= to; ++i) printf("%5d", a[i]); }

Billedserie: Scenarier der viser opdelingen i små og store elementer

Scenarier der viser opdelingen i små og store elementer

Billed nr. 1. Startsituationen forud for partitioneringen af tabellen. Deleelementet udvælges som det første. Variablen i tælles op sålænge elementerne er mindre end deleelementet. j tælles tilsvarende ned sålænge elementerne er større end deleelementet.

 

Billed nr. 2. Element i er større end deleelementet. Element j er mindre. De to ombyttes.

 

Billed nr. 3. Området med små og store elementer kan gøres lidt større efter ombytningen. i og j bevæges igen mod midten.

 

Billed nr. 4. i og j mødes...

 

Billed nr. 5. ... eller i og j overhaler hinanden.

 

Quicksort (4) Slide Indhold Stikord Referencer

En god implementation plejer at være blandt de allerbedste sorteringsmetoder - men der er ingen garanti

Køretid i bedste tilfælde: I størrelsesordenen n · log2 (n) sammenligninger og ombytninger. Køretid i værste tilfælde I størrelsesordenen n2 sammenligninger og ombytninger.

Tabel. En tabel der illustrerer forskellen på væksten af n2 og n · log2 (n)

n n2 n · log2 (n) 100 10.000 664 1000 1.000.000 9.966 10.000 100.000.000 132.887 100.000 10.000.000.000 1.660.964

Det kan vises at en sortering med i størrelsesordenen n · log (n) sammenligninger og ombytninger er optimal.

Opgaver Slide Indhold Stikord Referencer

Opgave 11.6. Opgave 1 side 587 i PSPD(8ed) - blob_count

Dette er hints til opgave 1 side 587 i Problem Solving and Program Design in C, 8ed (svarende til opgave 1 side 583 i 7ed). Der findes en video som giver et oplæg til problemløsningen. Jeg anbefaler at I ser denne video forud for løsningen af opgaven. Jeg synes det er mere naturligt at kalde funktionen blob_count i stedet for bogens forslag, blob_check. Bogens grid, vist nederst side 587 (8ed), kan laves på denne måde: int grid[5][5] = { {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, {0, 0, 1, 0, 1}, {1, 0, 0, 0, 1}, {0, 1, 0, 1, 1}, }; Med denne opskrivning er det mest naturligt at x 'er lodret' (betegner rækker) og at 'y er vandret' (betegner søjler). Dette syn er altså lidt anderledes end bogens. Bemærk at grid[0][0] er 1 (øverste venstre hjørne), grid[0][4] er 0 (øverste højre hjørne), grid[4][0] er 0 (nederste venstre hjørne), og at grid[4][4] er 1 (nederste højre hjørne). Overvej nøje, hvordan du vil håndtere felter som falder uden for griddet (f.eks grid[-1][5]). Hint: Lad blob_count på sådanne felter returnere 0. Som en centalt punkt i opgaven skal du besøge alle 8 naboer til et punkt i tabellen. Det kan være træls at gøre dette manuelt, nabo for nabo. Overvej hvordan dette kan gøres med (to nestede) for-løkker. Vær sikker på at funktionen blob_count bliver rekursiv. Altså at funktionen kaldes rekursivt på alle 8 naboer af en celle. Ideen er at tælle blob størrelsen af eksempelvis celle (x+1,y+1) efter nøjagtig samme opskrift som blev anvendt til at tælle blob størrelsen af celle (x,y). Som beskrevet i bogen er det nødvendigt at markere at en celle er talt. Dette gøres lettest ved at ændre 1-tallet til 0 i cellen. Dette ødelægger griddet. Jeg foreslår derfor at det givne grid kopieres over i et andet grid før kaldet af blob_count. På denne måde er det en kopi, som ødelægges, ikke originalen. Skriv gerne en copy_grid funktion, som udfører dette. I main bør du indlæse et (x,y) punkt og kalde blob_count på (x, y). Gør gerne dette i en løkke, så du kan undersøge flere (x,y) punkter i samme kørsel af programmet.

Opgave 11.6. Rekursive udgaver af Euclids algoritme

I denne opgave vil vi programmere iterative beregninger med brug af rekursion. Funktionerne, som skal programmeres i denne opgave, skal altså følge det mønster vi har set i funktionen iterative_factorial (et program i lektionen om rekursion). Vi har set iterative udgaver af Euclids algoritme i lektionen om gentagelse og løkker og vi har set en gcd funktion i lektionen om funktioner. Programmer først en rekursiv udgave af den version af Euclids algoritme, der er baseret på gentagen restberegning. Programmer dernæst en rekursiv udgave af den version af Euclids algoritme, der er baseret på gentagen subtraktion.

Kapitel 11: Rekursion
Kursets hjemmeside     Forfatteren's hjemmeside     Om frembringelsen af disse sider     Forrige lektion (top)     Næste lektion (top)     Forrige lektion (bund)     Næste lektion (bund)     
Genereret: 9. maj 2022, 14:00:12