I dette afsnit vil vi se på række simple eksempler på rekursion. Vi repeterer fakultetsfunktionen, rodsøgning og strengsammenligningen fra tidligere lektioner. Som nye eksempler vil vi se på en Fibonaccital funktion og en funktion til potensopløftning.

34.1 Eksempler fra tidligere lektioner 34.4 Fibonacci tal (3) 34.2 Fibonacci tal (1) 34.5 Potensopløftning (1) 34.3 Fibonacci tal (2) 34.6 Potensopløftning (2)

 

34.1.  Eksempler fra tidligere lektioner
Indhold   Op Forrige Næste   Slide Aggregerede slides    Stikord Programindeks Opgaveindeks 

Fakultetsfunktionen mødte vi i afsnit 14.1 i forbindelse med vores introduktion til rekursiv funktioner. I program 14.1 illustreres det hvordan den velkendte formel for fakultetsfunktionen (se teksten i afsnit 14.1) kan implementeres som en funktion skrevet i C.

Rodsøgningsfunktionen fra kapitel 13 er et andet godt og simpelt eksempel som appellerer til rekursiv tankegang. Den iterative løsning på rodsøgningsproblemet fra program 13.1 er vist som en tilsvarende rekursiv løsning i program 14.3. Personlig finder jeg at den rekursive løsning er mere elegant, og på et lidt højere niveau end den iterative løsning.

I program 34.1 viser vi en rekursiv løsning på strengsammenligningsproblemet, jf. afsnit 28.1, som har været en øvelse i en tidligere lektion af kurset. I en if-else kæde håndterer vi først en række randtilfælde samt situationerne hvor det første tegn i s1 og s2 er forskellige. I det sidste tilfælde kalder vi funktionen rekursivt (det røde sted). Vi håndterer her et delproblem, svarende til det oprindelige problem, på de dele af s1 og s2 som ikke omfatter de første tegn i strengene.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

int mystrcmp(const char* s1, const char* s2){
  int result;

  if (*s1 == '\0' && *s2 == '\0') 
    result = 0;
  else if (*s1 == '\0' && *s2 != '\0')
    result = -1;
  else if (*s1 != '\0' && *s2 == '\0')
    result = 1;
  else if (*s1 < *s2)
    result = -1;
  else if (*s1 > *s2)
    result = 1;
  else       /* (*s1 == *s2) */
    result = mystrcmp(s1+1, s2+1);

  return result;
}

I det følgende vil vi se på endnu flere eksempler som involverer rekursion.

34.2.  Fibonacci tal (1)
Indhold   Op Forrige Næste   Slide Aggregerede slides    Stikord Programindeks Opgaveindeks 

Der er et antal 'sikre hits', som næsten altid findes blandt eksemplerne, som bruges til at illustrere rekursive løsninger. Beregningen af Fibonacci tal er en af disse. Et Fibonaccital er summen af de to foregående Fibonacci tal. Starten kan i princippet være vilkårlig. I vore eksempler er fib(0) = 0 og fib(1) = 1.

Det er ikke svært at programmerer en funktion, som returnerer det n't Fibonacci tal. I program 34.1 viser vi en flot rekursiv udgave, som er en ganske direkte nedskrivning af definitionen givet herover.

1
2
3
4
5
6
7
8
9
10
11
12

long fib(long n){
  long result;

  if (n == 0)
    result = 0;
  else if (n == 1)
    result = 1;
  else
    result = fib(n-1) + fib(n-2);

  return result;
}

Læg mærke til at hvert kald af fib forårsager to nye kald af fib. Denne observation er kritisk når vi skal forstå, hvorfor et kald af fib, f.eks. fib(45), tager adskillige minutter at gennemføre.

På slide udgaven af dette materiale linker vi til en komplet program, som udskriver de 100 første Fibonaccital. Programmet er også her. Dette program vil aldrig køre til ende på grund af ovenstående observation. Køretiden af fib udvikler sig eksponentielt. I praksis betyder dette, at der er en øvre grænse for hvilke kald af fib der overhovedet kan beregnes med metoden i program 34.2.

Vi viser en let modificeret udgave af fib funktionen i program 34.3 herunder. I denne udgave tæller vi antallet af additioner, som udføres af et kald af fib samt alle de deraf afledte rekursive kald. Læg mærke til at tælleren plus_count er en global variabel (det røde sted). Variablen tælles op for hver addition (det blå sted), og den nulstilles for hvert nyt ydre kald af fib (det brune sted).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <stdio.h>

long plus_count = 0;

long fib(long n){
  long result;

  if (n == 0)
    result = 0;
  else if (n == 1)
    result = 1;
  else {
    result = fib(n-1) + fib(n-2);
    plus_count++;
  }

  return result;
}

int main(void) {
  long i, fib_res;

  for(i = 0; i < 42; i++){
    plus_count = 0; 
    fib_res = fib(i);
    printf("Fib(%li) = %li (%li)\n", i, fib_res, plus_count  );
  }
   
  
  return 0;
}

Når vi kører program 34.3 ser vi at værdien af variablen plus_count vokser i samme takt som værdierne af fib funktionen anvendt på større og større inputværdier. Herunder viser vi et udsnit af output fra program 34.3.

Fib(0) = 0 (0)
Fib(1) = 1 (0)
Fib(2) = 1 (1)
Fib(3) = 2 (2)
Fib(4) = 3 (4)
Fib(5) = 5 (7)
Fib(6) = 8 (12)
Fib(7) = 13 (20)
Fib(8) = 21 (33)
...
Fib(36) = 14930352 (24157816)
Fib(37) = 24157817 (39088168)
Fib(38) = 39088169 (63245985)
Fib(39) = 63245986 (102334154)
Fib(40) = 102334155 (165580140)
Fib(41) = 165580141 (267914295)

Vi cutter listen på det sted, hvor udførelsen af fib bliver virkelig langsom. Vi ser og mærker tydeligt, at arbejdet i fib vokser eksponentielt i forhold til parameteren n.

34.3.  Fibonacci tal (2)
Indhold   Op Forrige Næste   Slide Aggregerede slides    Stikord Programindeks Opgaveindeks 

Vi vil nu i yderligere detalje forstå hvorfor fib er så langsom. I figur 34.1 ser vi kaldene af fib(5) . Hvert kald af fib resulterer i to nye kald, på nær kald af fib(0) og fib(1). Antallet af knuder et træet fib(n) bliver astronomisk stor når n vokser. Da der udføres én addition pr. indre knude i træet vokser beregningsbyrden tilsvarende. Reelt er det dog vigtigt at forstå, at langt de fleste beregninger er genberegninger af allerede beregnede værdier af fib(n).

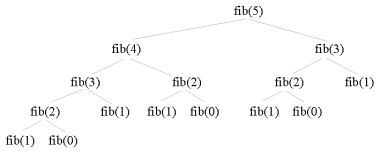
Figur 34.1    En illustration af beregningsprocessen af fib(5)

Mere effektive løsninger En simpel iterativ løsning En rekursiv løsning, som kortslutter genberegningerne

Vi ser på to mere effektive løsninger i næste afsnit.

34.4.  Fibonacci tal (3)
Indhold   Op Forrige Næste   Slide Aggregerede slides    Stikord Programindeks Opgaveindeks 

Den mest oplagte - men også den mindst interessante - effektivisering er programmering af fib med en forløkke. Denne udgave er vist i program 34.4.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include <stdio.h>

long fib(long n){
  long small, large, temp, m;

  for (small = 0, large = 1, m = 0;
       m < n;
       m++){
    temp = small;
    small = large;
    large = large + temp;
  }

  return small;
}

int main(void) {
  long i;

  for(i = 0; i < 100; i++){
    printf("Fib(%li) = %li\n", i, fib(i) );
  }
   
  
  return 0;
}

I program 34.4 har vi variablene small og large, som på et hvert tidspunkt indeholder hhv. fib(n) og fib(n+1) for et eller andet heltal n. Variablene small og large opdateres stort set på samme måde som de to variable p og q i proceduren swap, jf. program 23.2.

Herunder ser vi en udgave af fib, som minder meget om program 34.2. Forskellene fremgår af de blå, røde og lilla programsteder. Vi har indført et array, memo, som indeholder allerede beregnede værdier af fib(n). I stedet for at genberegne fib(n) hentes det ud af tabellen memo (det røde sted). Vi skal naturligvis også huske at putte nyberegnede værdier af fib(n) ind i memo (det lilla sted). Bemærk at rækkefølgen af tilfældene i if-else kæden er vigtig at iagttage.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

#include <stdio.h>


long fib(long n){
  long result;
  static long memo[100];   /* elements pre-initialized to 0 */

  if (n == 0)
    result = 0;
  else if (n == 1)
    result = 1;
  else if (memo[n] != 0)
    result = memo[n];
  else {
    result = fib(n-1) + fib(n-2);
    memo[n] = result;
  }

  return result;
}

int main(void) {
  long i;

  for(i = 0; i < 100; i++)
    printf("Fib(%li) = %li\n", i, fib(i));
  
  return 0;
}

Hermed afslutter vi vores interesse for Fibonacci tal.

34.5.  Potensopløftning (1)
Indhold   Op Forrige Næste   Slide Aggregerede slides    Stikord Programindeks Opgaveindeks 

Potensopløftning handler i bund og grund om at gange et tal med sig selv et antal gange. Vi starter med at se på en simpel, ligefrem og rekursiv potensopløfningsfunktion. I afsnit 34.6 ser vi på en meget mere interessant og meget bedre udgave.

Den beregningsmæssige idé er vist herunder. Bemærk at vi f.eks. tillægger 2^-3 betydning, nemlig som 1/2³.

Beregningsidé: potens > 0:         tal potens = tal potens-1 · tal potens = 0:         tal 0 = 1.0 potens < 0:         1.0 / tal -potens

Idéen er direkte og meget ligefrem implementeret i program 34.6 herunder.

1
2
3
4
5
6
7
8
9
10
11
12

double power(double number, int pow){
  double result; 

  if (pow == 0)
    result = 1.0;
  else if (pow > 0)
    result = number * power(number, pow - 1);
  else 
    result = 1.0 / power(number, -pow);

  return result;
}

34.6.  Potensopløftning (2)
Indhold   Op Forrige Næste   Slide Aggregerede slides    Stikord Programindeks Opgaveindeks 

Løsningen i program 34.6 var ganske naiv. Det er måske overraskende at der kan udtænkes en rekursiv løsning som er meget mere effektiv uden at være ret meget mere kompliceret. Ideen i den nye løsning er beskrevet på matematisk vis herunder.

Beregningsidé: potens > 0, potens er lige:         tal potens = ( tal potens/2 ) 2 potens > 0, potens er ulige         tal potens = tal potens-1 · tal potens = 0:         tal 0 = 1.0 potens < 0:         1.0 / tal -potens

Den essentielle indsigt er at opløftning i en lige potens p kan udføres ved at opløfte til potensen p/2 efterfulgt at en kvadrering. I stedet for at udføre p multiplikationer skal vi nu kun udføre arbejdet forbundet ved opløfning i p/2 potens efterfulgt af en kvadrering. Hvis p/2 igen er lige kan vi igen halvere. Hvis p/2 er ulige ved vi at (p/2)-1 er lige. Så "tricket" kan typisk gentages flere gange - rekursivt. Kvadrering består naturligvis af en enkelt multiplikation.

Programmet herunder er en direkte og ligefrem implementation af ovenstående formler.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

double power(double number, int pow){
  double result; 

  printf("power(%lf,%i)\n", number, pow);
  if (pow == 0)
    result = 1.0;
  else if (pow > 0 && even(pow))
    result = sqr(power(number,pow/2));
  else if (pow > 0 && odd(pow))
    result = number * power(number, pow - 1);
  else 
    result = 1.0 / power(number, -pow);

  return result;
}

På en separate slide i materialet leverer vi dokumentation for fordelene ved program 34.7 i forhold til program 34.6. Det sker ved et billedserie som viser de rekursive kald i power(2.0,10). Vi viser også et komplet program som kalder både power ala program 34.6 og power ala program 34.6. Udskriften af programmet viser antallet af multiplikationer i en lang række kald. Det fremgår klart, at antallet af multiplikationer i den "smarte udgave" vokser meget langsomt i forhold til potensen. Væksten viser sig at være logaritmisk, idet vi i mindst hver andet kald halverer potensen.