Examples

Traffic Dilema

Suppose we need to travel to Sidney from Aalborg as soon as possible but we are not sure which mode of transport is the fastest: a bike, a car or a train. Each of them have different speeds and risks depending on traffic conditions. Below is a stochastic timed automaton capturing trip possibilities:

We start in the location Aalborg on the left, pack our things and leave within 2 time units. Then we can choose/control our prefered mode of travel:

Bike is relatively slow but it is the most predictable option which takes to Sydney in between 42 and 45 time units and thus depends very little on uncontrollable traffic conditions.
Car has a possibility of an Easy and fast trip in 20 time units if traffic permits (probability weight 10 yields likelyhood of 10/11), but there is a risk of 1 in 11 to get stuck in Heavy traffic and thus the trip could be prolonged up to 140 time units.
Train have periodic schedules and thus may have a waiting time up to 6 time unitsand it is quite likely (10 out of 11) that we will board the train successfully and spend up to 35 time units in location Go before reaching Sydney. There is also a small risk (1 out of 11) that the train is canceled and we end up in Wait, where we would have to decide either to switch to another train or GoBack home and in Aalborg make a decision again.

Given our model, we can inspect sample trip trajectories via SMC simulate query where the locations are encoded as different levels:

simulate 1 [<=100] { 
     Kim.Aalborg +  2*Kim.Bike +  4*Kim.Easy +  6*Kim.Heavy + 
     8*Kim.Train + 10*Kim.Go +   12*Kim.Wait + 14*Kim.Sydney }

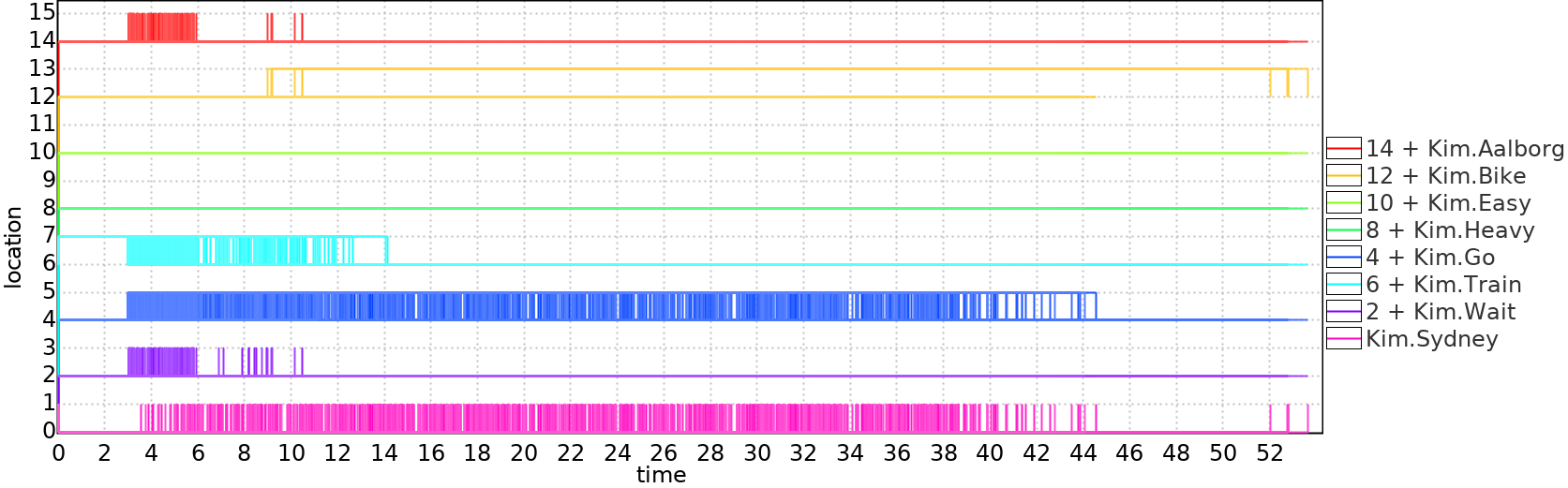
Below are two sample trajectories computed by Uppaal Stratego:

Normal train trip in 20 t.u.:	Train and then bike in 50 t.u.:

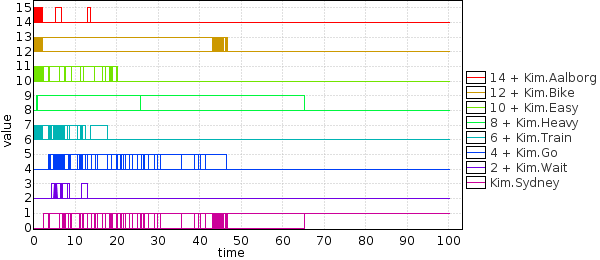
The following query and resulting plot shows where and when most of the time is being spent:

simulate 100 [<=100] {
     14+Kim.Aalborg, 12+Kim.Bike, 10+Kim.Easy, 8+Kim.Heavy,
      6+Kim.Train,    4+Kim.Go,    2+Kim.Wait, Kim.Sydney }

Generate and evaluate a safe strategy to get to Sydney within 50 time units:

strategy GoSafe = control: A<> Kim.Sydney && time<=50

simulate 100 [<=100] {
     14+Kim.Aalborg, 12+Kim.Bike, 10+Kim.Easy, 8+Kim.Heavy,
      6+Kim.Train,    4+Kim.Go,    2+Kim.Wait, Kim.Sydney } under GoSafe

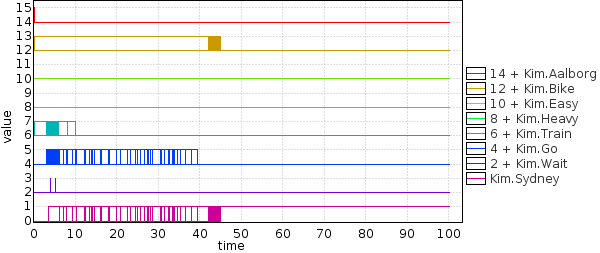
The plot shows that most of the time is spent in Bike and Sydney, therefore Bike is the sure way to reach Sydney given the strict time bound.

Learn fast strategy by minimizing the time to get to Sydney:

strategy GoFast = minE (time) [<=200] : <> Kim.Sydney

simulate 100 [<=100] {
     14+Kim.Aalborg, 12+Kim.Bike, 10+Kim.Easy, 8+Kim.Heavy,
      6+Kim.Train,    4+Kim.Go,    2+Kim.Wait, Kim.Sydney } under GoFast

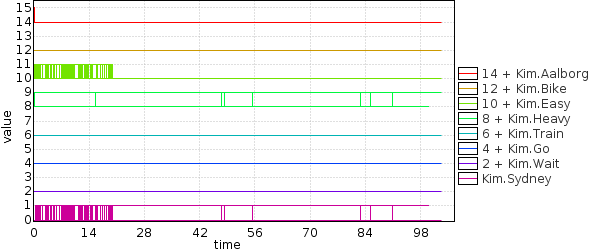
The plot shows that most of the time is spent in Easy and Heavy and then Sydney, therefore Car is the fastest choice on average.

Optimize the safe strategy by minimizing the time to get to Sydney:

strategy GoFastSafe = minE (time) [<=200] : <> Kim.Sydney under GoSafe

simulate 100 [<=100] {
     14+Kim.Aalborg, 12+Kim.Bike, 10+Kim.Easy, 8+Kim.Heavy,
      6+Kim.Train,    4+Kim.Go,    2+Kim.Wait, Kim.Sydney } under GoFastSafe

The result is similar to the safe solution above, meaning that there were not enough options to minimize the time while using the safe strategy.

There are many more queries to evaluate the generated strategies (e.g. computing the probability of reaching Sydney and the average time needed to reach Sydney). The model and queries can be downloaded here: traffic.xml.

Newspaper and Travel

Model: newspaper.xml