Exercises
- BRICK sorter
- Coffee machine
- Smart Light
- Protocol
- Veritication Options
- Over approximation
- Active clock reduction
- Test automata
- Data Link Protocol
- Theory
- The CSMA/CD Protocol
- Protocol
- The CSMA/CD Protocol continued
- Gossiping Girls
- Reduction
- Solving constraint systems
- Representation of regions
- Druzba
- Train-Gate Debugging
- Jug Filling
- Rush Hour
- Crossing the River
- How much can we loose?
- How much can we reach?
- A simple vending machine
- An extended vending machine
- The full vending machine.
Exercise
1 (BRICK sorter)
Experiment with the BRICK Sorter model (.xml) in UPPAAL. Experiment with the model of the environment (including the number of bricks) to find out:
- under which circumstances the sorter operates correctly?, and
- under which circumstances the sorter misbehaves?
Use the functionalities of UPPAAL to explain what happens when the sorter misbehaves.
Change the model of the controlling tasks in order to ensure correct sorting of 2 bricks.
Exercise 2 (Coffee Machine)
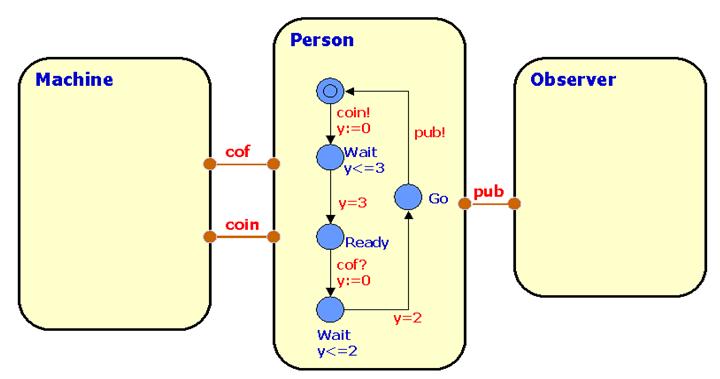
In this exercise you are asked to design the control of a Machine (the control program) which will serve a coffee craving Person (the environment). As you can see above the person repeatedly (tries to) insert a coin, (tries to) extract coffee after which (s)he will make a publication. Between each action the person requires a suitable time-delay before being ready to participate in the next one.
The machine takes some time for brewing the coffee and will time-out if coffee has not been taken before a certain upper time-limit.
As a requirement we want the overall behaviour to ensure that the indicated Observer experiences a constant flow of publications from the system. In particular we want the Observer to complain if at any time more than 8 time-units elapses between two consecutive publications. Model the Machine and Observer in UPPAAL and analyse the behaviour of the system. Try to determine the maximum brewing time allowed by the Machine in order that the above requirement is met.
Exercise 3 (Smart Light)
Reconstruct a model of the Smart Light Switch (Intelligent Light Control) taking timing into account. Below you see (from the lecture) a timed automata model of the interface between the user and the control program. Complete the model by designing appropriate automata for the control program. Simulate the model and try to estimate the minimum time to take the light to its maximum intensity.
Exercise 4
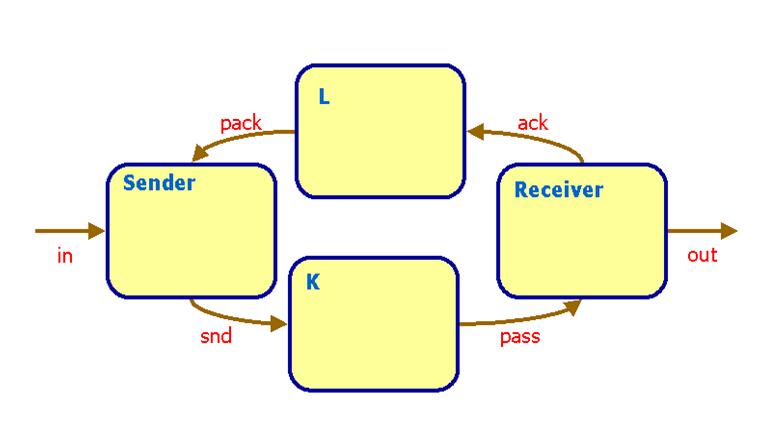
Consider the above system, where a SENDER and a RECEIVER wants to communicate over a potential faulty communication line. In order to allow the SENDER to detect when communication succeeds, two (potentially faulty) communication media are used: one (K) for transmitting the message from SENDER go RECEIVER and one (L) for transmitting acknowledgements from the RECEIVER to the SENDER. We assume that the both media are one-place buffers. Also, we shall pay no attention to the actual message being communicated.
Use UPPAAL to model and analyse communication systems of the above type, where the media
- are lossy
- have delays
The desired behaviour of the overall system is that of a one-place buffer. Use UPPAAL to examine to what extent this behaviour is meet in the various scenarios above.
Exercise 5 (Verification Options)
Experiment with the various verification options of UPPAAL on Fischers Protocol(.xml, .q), The Soldiers Problem (.xml, .q) and the Gear Box Controller (.xml, .q). Estimate the verification times required and try to conclude on which options are to be prefered on which examples.
Exercise 6 (Over-Approximations)
Construct an example where use of the verification option 'Over-approximation' gives the wrong answer.
Try to make your example as small as possible.
Exercise 7 (Active Clock Reduction)
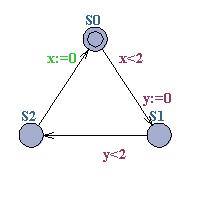
Consider the timed automaton below:
Calculate the active clocks for the three locations, S0, S1 and S2. Compute the reachable symbolic state-space of the timed automaton (using canonical DBM's for representing constraint systems) first without any reduction and afterwards with Active-clock reduction. Compare the number of constraints and symbolic states required to represent the reachable state-space in the two cases.
Exercise 8 (Test automata)
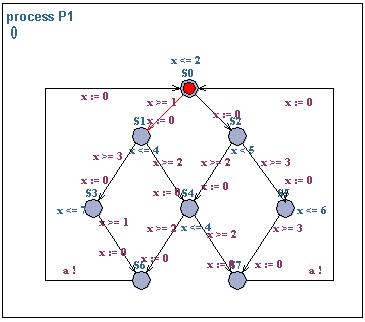
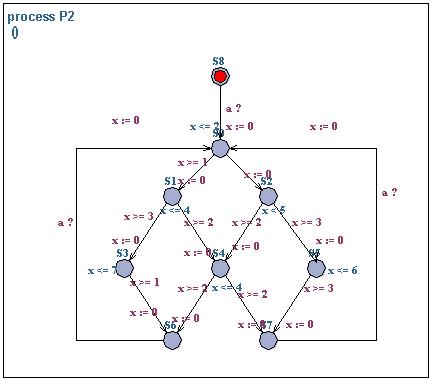
Consider the two timed automata P1 and P2 above. The automata are interacting over an urgent channel a. Use the testautomata or decoration technique for analysing bounded liveness properties of the form:
- whenever P1.S1 then P2.S0 within t timeunits,
- whenever P1.S0 then P2.S4 within t timeunits,
- whenever P1.S0 then P2.S0 will not occur before t timeunits.
You can find downloadable version of the system here (.xml.
Exercise 9 (Modeling)
In this exercise you are to model, validate and verify a simple data link protocol, where some unrealistic assumptions will be made in order to keep the exercise simple.
The protocol specification is as follows: there are a Sender, a Receiver and a Medium.
The medium can after reception of a message from the sender, do one of two things: either the message is delivered to the receiver, or it is lost. The loss of a message should be modeled by an internal transition (unlabelled transition in UPPAAL), since the loss itself does not constitute an observable event. When a message is lost a time-out in the sender will occur - model this time-out as a communication signal sent from the medium (in case of message loss) to the sender. In case of a time-out, the sender will retransmit the message. When the receiver gets a message an acknowledgment is sent to the sender. Assume that the acknowledgment is sent directly to the sender and not through any medium.
Task 1: Model the above protocol in UPPAAL, and validate using the simulator that it is functionally correct.
Redefine the protocol by modifying the receiver so that it reports to the layer above when a message is receive. Add a test process (to model the above layer) that receives the messages from the receiver. Modify the sender to receive messages from the layer above. Add another test process that generates messages to the sender (modeling the above layer).
Task 2: Validate that the functionality of the refined protocol is correct using the simulator.
Now modify the test environment so that the test sender increments a shared integer variable i whenever a message is sent. Modify the test receiver so that it decrements the variable i whenever a message is received.
Task 3: Validate the protocol and verify that the value of the variable i is always one or zero.
Task 4: What happens if the protocol is redefined in the following way: acknowledgments are not sent at all from the receiver to the sender? What happens if additionally the sender never expects acknowledgments? Validate, verify and describe in words the behavior of the resulting protocol.
Model the content of messages as (bounded) integer values and change the models of the protocol and the test environment consequently.
Task 5: Validate and afterwards verify, that the content of a message when sent equals the content of the message when received.
Exercise 10 (Theory)
JPK exercises 17, 18, 22.
Exercise 11 (Modeling, The CSMA/CD Protocol)
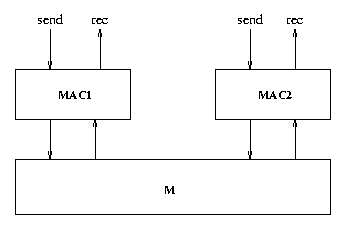
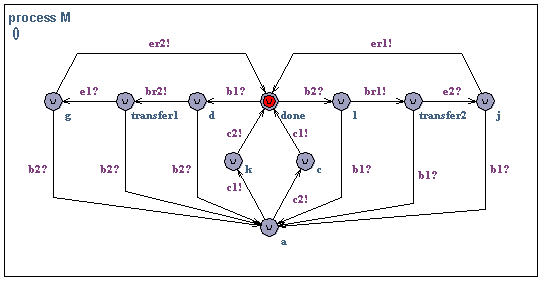
In this exercise you will study the Media Access Control (Mac) sub layer of the Carrier Sense, Multiple Access with Control Detection (CSMA/CD) communication protocol. The protocol specification consists of two MAC entities, MAC1 and MAC2, interconnected by a bi-directional medium M. The MAC entities are identical and can both transmit and receive messages over the medium. This means that collisions may occur on the medium (if the two MAC's transmit simultaneously). It is assumed that collisions will be detected in the medium and signaled to both MAC1 and MAC2.
Overview of the MAC sub layer.A model of the protocol is given in csma-cd-start.xml (the specification is taken from "Verifying a CSMA/CD Protocol with CCS" by Joachim Parrow. The specification uses the following synchronization actions to describe the protocol events:
- send - service provided by Mac which reacts by transmitting a message,
- rec - (receive) service provided by Mac, indicates that a message is ready to be received,
- b - (begin) Mac begins message transmission to M,
- e - (end) Mac terminates message transmission to M,
- br - (begin receive) M begins message delivery to Mac,
- er - (end receive) M terminates message delivery to Mac,
- c - (collision) Mac is notified that a collision has occurred on M.
Note that a message transmission is not modeled by a single action. Instead the start of a transmission and the end of a transmission are modeled by two separate actions (the actions b(r) and e(r)). This is needed as there may be collisions detected in the middle of a transmission. Note also that we use indexes on all actions as there are two identical MAC entities.
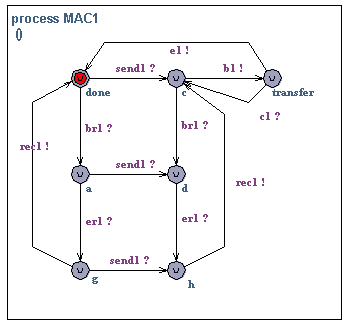
MAC1.Initially, MAC1 accepts a service call (send1?). The MAC initiates transmission (b1!), unless a message is in the process of being received. If the transmission is successfully terminated (e1!) new messages can be transmitted and the process is repeated. If a collision occurs (c1?) the MAC attempts re-transmission of the message. In all states (except when a message is being transmitted) the MAC is willing to start receiving. A message may be received (br1?) after which the MAC may not begin message transmission before the end of message (er1?) has been received and the MAC has signaled that the message is ready to be delivered (rec1!). However, the MAC may receive a send request (send1?) if there is not already another request waiting.
The medium M.Initially, the medium accepts transmission from one of the MAC's (b1? or b2?). We assume MAC1 (b1?) starts transmitting first (the case for b2? is symmetric). The medium is assumed to be "half-duplex" meaning that a full message must be transmitted (br2!, e1?, er2!) before the next message can be accepted. If the receiving MAC (i.e. MAC2) starts transmission (b2?) the medium interrupts the transmission and signals collision (c1!, c2!) to both MAC1 and MAC1 (in any order).
Task 1: Open the protocol specification in csma-cd-start.xml and add a test environment that "uses" the protocol. Validate that your system is functionally correct using UPPAAL's simulator.
Task 2: Check (by verification) if the system is correct in the sense that sent messages are received. How many messages can be in transfer at the same time? Is it 1, 2 or more messages?
The model of the MAC is slightly inaccurate. In reality, a MAC would be two processes: one sender performing the actions send!, b!, e!, c? and one receiver performing the actions rec!, br? and er?
Task 3: Refine the protocol by letting each MAC consist of two processes, a sender (S) and a receiver (R). The idea is to let S perform all "horizontal" transitions and R all "vertical" transitions. Replace MAC with S and R. Use UPPAAL to validate and verify that the protocol no longer is correct.
Task 4: Redefine the protocol again so that it works, while still keeping the S and R separate. This is a bit tricky. You may need to add some synchronization channels (or data variables) to achieve synchronization between S and R.
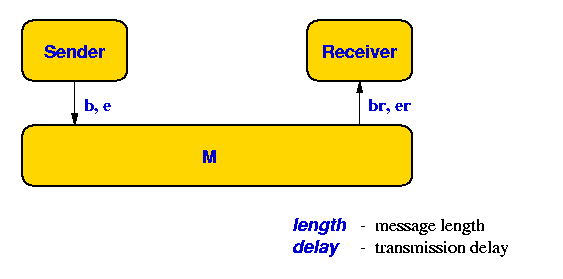
Exercise 12 (Modeling)
In this exercise you are asked to model a communication medium M, a Sender, and a Receiver. The sender sends messages of a fixed length length, which is the time between the beginning and the end of a message. The medium has a transmission delay delay, which is the time between the beginning (or end) of a message is sent and the beginning (or end) of a message is received. For example, if the beginning of a message is sent at time t, it will be received by the receiver at time t+delay.
Task 1: Model the system as a network of timed automata in UPPAAL. Assume length<delay. Model the beginning and end of each message. It is recommended to use integer constants in UPPAAL for the values length and delay.
Task 2: Validate the sytem in the simulator and find out what the total timed between "begin send" and "end receive" is.
Task 3: Modify the medium M to handle messages of length length>=delay.
Exercise 13 (Modeling: the CSMA/CD Protocol continued)
In this exercise we use the model of the CDMA/CD protocol. You are asked to refine the model so that the sent messages have a fixed length of time length, and to refine the communication medium M to have a communication delay of time delay..
Task 1: Model/modify the system with the assumption length<delay.
Task 2: Verify that the system is correct in the sense that all sent messages are indeed received..
Task 3: Refine the medium to allow messages of length length>=delay.
Task 4: Verify that the refined system is correct in the sense that all sent messages are indeed received.
Exercise 14 (Gossiping Girls)
Model and analyze the following gossiping girls problem in UPPAAL. A number of girls initially know one distinct secret each. Each girl has access to a phone which can be used to call another girl to share their secrets. Each time two girls talk to each other they always exchange all secrets with each other (thus after the phone call they both know all secrets they knew together before the phone call). The girls can communicate only in pairs (no conference calls) but it is possible that different pairs of girls talk concurrently.
Your tasks are as follows:
- Model the problem as a network of UPPAAL timed automata and use UPPAAL to find the minimal number of phone calls needed for four girls to know all secrets.
- Refine your model so that each phone call lasts exactly 60 seconds (for simplicity this time duration is irrelevant of the number of exchanged secrets). Find the minimum time needed to solve the gossiping girls problem for four girls.
- Experiment with the UPPAAL search options breath-first and depth-first search, upper and lower approximations, and with the diagnostic trace settings fastest and shortest. Try to solve the problem for five girls.
- (For the keenest) Modify the model so that so that calls are asynchronous (i.e. only the caller tells the receiver her secrets and not vise versa).
Hint:
- Design a single template for all girls.
- For each girl, you may choose to remember the currently known secrets either in a local array of booleans or using an integer variable (use a binary encoding such that if a girl knows the secrets of e.g. girls 1 and 3 but does not know the secrets of girls 2 and 4, the value in the integer variable will be (0101) binary = 5; you might find useful the operation | for a bitwise OR).
Exercise 15 (Reduction)
This exercise will (hopefully) convince you that reachability checking in the UPPAAL-model is a hard problem indeed (NP-hard); if fact consider how you could use UPPAAL to analyse satisfiability of propositional logic formulas, i.e. formulas F build from propositional variables, b1, b2, b3,...... using boolean connectives (and, or, negation, ....). You may assume that F is in conjunctive normal form that is
F = C1 and C2 and C3 and ....... and Cn, where
Ci = Li1 or Li2 or Li3 or ......... or Lik, where
Lij is a variable bi or a negated variable ~biApply your idea for a construction to the formula:
(x or y or ~z or u) and (~x or y or z or ~u) and ( x or ~y or ~z) and (~x or y or ~u)
to see if the formula is satisfiable and if so to obtain a satisfying assignment to the boolean variables x, y, z and u.
Exercise 16 (Solving constraint systems)
The reachability algorithm of UPPAAL is based on efficient representation and manipulation of Difference Constraints Systems, i.e. linear equation systems between clock values where each constraint is of the simple form (xj - xj) <= bk.
In this exercise you should think about how to use UPPAAL to decide whether a given difference constraint system has solutions or not. Use your method to decide whether the following systems have solutions or not. In case there are solutions try to use UPPAAL to exhibit a single solution:
System 1: x1-x2<=1, x3-x1<=-1, x1-x4<=3, x2-x3<=5.
System 2: x1-x2<=1, x1-x4<=-4, x2-x3<=2, x2-x5<=7, x2-x6<=10, x4-x2<=2, x5-x1<=-1, x5-x4<=3, x6-x3<=-8.
Consider also how to use UPPAAL to check for two difference constraint systems D1 and D2 whether all solutions to D1 are also solutions to D2. Use your 'method' to check whether the constraint system 1 above is included in the following system 3:
System 3: x1-x3<=7, x3-x4<=2, x3-x2<=4.
Exercise 18 (Druzba Mutex Problem)
Recall the Druzba mutex problem illustrated below.
.
The erroneous model is given to you as well as the query-file. Correct the model and supplement the query-file so that you obtain a satisfactory system (and verifiable so).
Exercise 19 (Train-Gate Error
Correction)
The following contains an erroneous version of the train-gate example. Here is the appropriate query-file.
Use UPPAAL (simulation, verification) to pin-point and explain the error(s). Having corrected the errors what is the minimum time one can guarantee between a train requesting access to the crossing and actually getting there?
Exercise 20 (Jug Filling)
Consider the one-player Jug game illustrated below. In this
instance, two jugs are given with capacities 5 and 3 respectively.
Initially, the two jugs are empty. Now legal actions/rules on the jugs
are fill (we assume an infinite capacity tap by which we may fill any
jug to the rim), empty (we may at any time empty the complete content of
a jug on the floor), and pour the content of one jug into the other (of
course stopping the pouring if and when the rim is reached). Given this
initial configuration, and legal rules, we want to figure out whether it is
possible to reach a situation where the content of one jug is exactly 1.
Make a scalable model of the Jug game in UPPAAL (i.e. allowing for arbitrary
numbers of jugs with arbitrary capacity) and use it to find solutions bringing
the above instance into a final configuration where the large jug contains 2
units, 3 units, 4 units, and where the large jug contains 3 units and the small jug contains 2 units.
Exercise 21 (Rush Hour)
In this exercise you are
asked to model a solitair game and solve use UPPAAL to solve the puzzle. The
game is simple. You have a 6x6 board like shown on the picture below. On the
board you find a number of cars of different size (personal vehicles and
trucks). The goal of the game is to move the cars by driving forward and
backwards in such a way that the red car can leave the board at the exit on the
right side of the board. The cars cannot turn!


Task 1: Make a model of the game in UPPAAL.
Task 2: Use your model to solve the two
puzzles shown in he second picture. What is the shortest
number of steps/moves needed to solve the puzzle?
Task 3: Extend your model with timing
constraint. Assume that it takes a different amount of time to move the cars,
e.g. 2 time units for the small ones and 3 for the trucks (you can also choose
to give each car its own time). Try to experiment with different assumptions as
to the number of hands/drivers, i.e. how many cars can move at the same time.
Task 4: Use Uppaal to find the fastest way of solving the puzzle (not
measured in computation time, but in time it take to move all the cars). Tip:
Use Uppaals diagnostic trace feature and ask for the fastest trace.
For the
keenest: you may
want to deal with the more challenging RAILROAD Rush Hour, which is on a 7x7
boards and with 2x2 blockers that can move bort horizontal and vertical (see
figure below):
Exercise 22 (Crossing the River)
Help a familly to cross a
river according to the following constraints:
- Max 2
persons on the boat,
- Mom not
alone with boys,
- Dad ont
alone with girls,
- Thief not
alone with family,
- Only
police officer, dad and mom can handle the boat.

Task 1: Make an Uppaal model of it and
generate a feasible schedule.
Task 2: Add temporal constraints (e.g. each
adult take a certain time to cross the river with the boat) and try to find the
quickest possible schedule.
Task 3: Try other parameters and constraints
for this game. Determine what is the feasibility limit depending on the number
of boys, girls, prisonners.
Exercise 23 (How much can we loose)
Consider the following
algorithm containing two parallel processes both incrementing a common
variable:
int n=0;
(n := n + 1 || n := n + 1)
In case the underlying
computational model execute n:=n+1 as an atomic operation the post condition is
that n=2. But in case n:=n+1 is executed as a number of atomic operations the
post condition becomes 1 ≤ n ≤ 2.
Now we generalize the problem
with respect to the number of increments done by each processor. Consider the
following algorithm in which n:=n+1 is a non atomic operation, i.e. n:=n+1 is
composed of the following sequence of three atomic updates: r:=n;
r:=r+1; n:=r where r is a register local
for the given parallel process:
const int
k=…; int n=0;
Process P
do
n := n+1
k times
end P
( P || P )
For k=1, this program is
equivalent to program 1. Obviously (why?) the final value of n can
not exceed 2*k. Intuition leads us to believe that k is the smallest
possible final value of n! However, this intution is wrong. Use
UPPAAL to model the above scenario (e.g. with k=10) and use model-checking to
find the smallest possible final value of n. Try to increase the
number of processes (e.g. consider ( P||P||P )).
Exercise 24 (How much can we reach)
Again we are considering the
paralle execution of two, simple (and identical) sequential programs:
const int n=1;
Process P
do
n := n+n
forever
( P || P )
Given that n:=n+n was atomic
the possible values of n during execution would be (all) powers of 2.
However, consider the situation when the update n:=n+n is carried out as the
following sequence of three atomic updates: r:=n; r:=r+n; n:=r.
Now the question as to which values n may achieve during execution is no longer
obvious. Model the above scenario in UPPAAL and try to figure out whether
(and how) n can achieve the values 2, 3, 8, 9, and 23. Which (and
why) values can n achieve?
Exercise 25 (Simple Vending Machine)
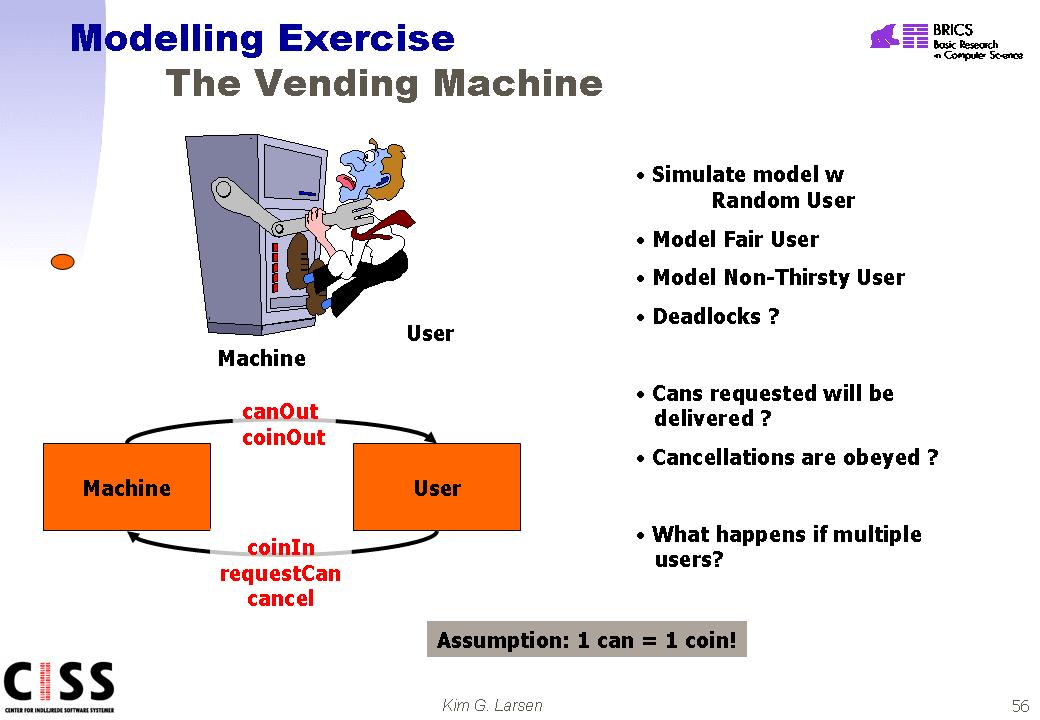 In this
exercise you are required to model a (very) simplified vending machine for
beverage cans. The vending machine is supposed to sell cans (containing
some interesting substance) to customers. In this simplest version, the
machine only sells a single kind of cans where a can cost one single unit (of
the currency of your choice). We also assume that the vending machine has
an unlimited number of available cans. Purchasing a can is usually
performed as follows:
In this
exercise you are required to model a (very) simplified vending machine for
beverage cans. The vending machine is supposed to sell cans (containing
some interesting substance) to customers. In this simplest version, the
machine only sells a single kind of cans where a can cost one single unit (of
the currency of your choice). We also assume that the vending machine has
an unlimited number of available cans. Purchasing a can is usually
performed as follows:
1. The
customer inserts a coin into the machine
2. The
customer may now either
- request a can, or
- cancel
3. Depending
on the order of the customer the vending machine should either provide a can or
return the coin.
Model in UPPAAL the vending machine. Also make models of various
types of customers including a random customer (may at any given moment
non-deterministically try to insert a new coin, cancel an order, ...etc), a
fair customer (behaving as intended by the machine), a non-thirsty user (always
cancelling after insertion of coin). Validate the various configurations
(machine and a particular customer) by simulation. Check for (absence) of
deadlock in your model. Try to verify that cans reqeusted will be
delivered, and cancellations are objeyed. What happens if the
configuration involves multiple users (possibly of different type)?
Exercise 26
(Extended Vending Machine)
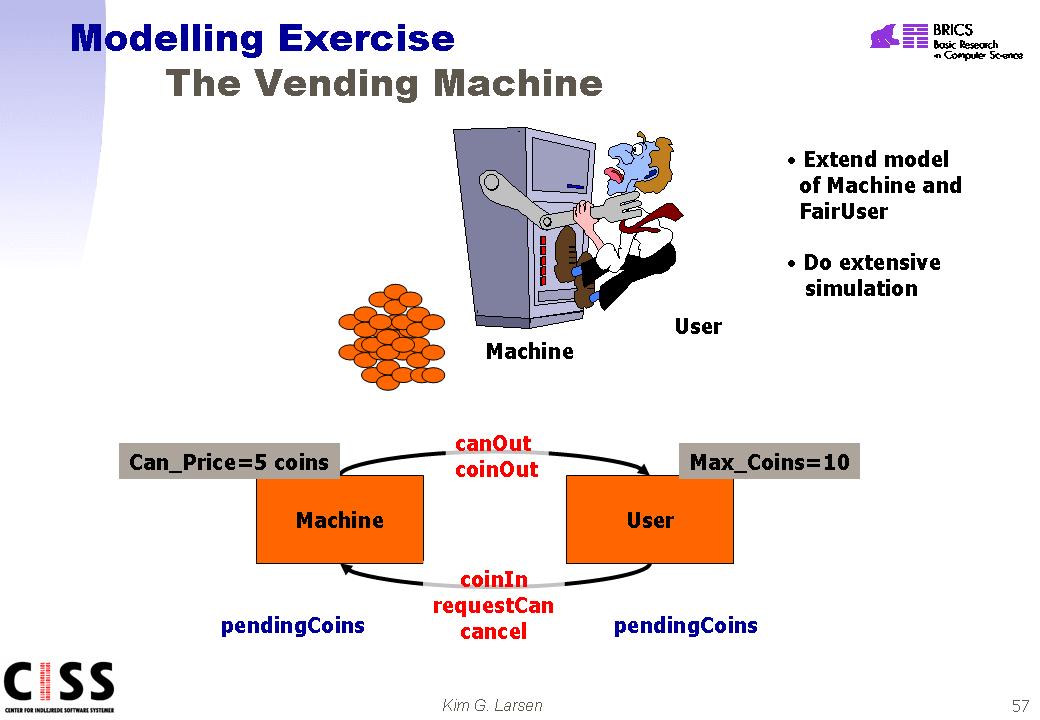 Extend the
model of the vending machine from the previous exercise so that the price
of a can is 5 units (or coins). Also change the behaviour of the
customers so that mulitple coins may be inserted before reqeusting a can is
attempted -- both the machine and the user should have their own local variable
(pendingCoins) for recording the credit of the customer. When a can is
requested the surplus of coins should be given back to the customer. To
make matters simpler you may assume that the user has a limited number of coins
(say 10).
Extend the
model of the vending machine from the previous exercise so that the price
of a can is 5 units (or coins). Also change the behaviour of the
customers so that mulitple coins may be inserted before reqeusting a can is
attempted -- both the machine and the user should have their own local variable
(pendingCoins) for recording the credit of the customer. When a can is
requested the surplus of coins should be given back to the customer. To
make matters simpler you may assume that the user has a limited number of coins
(say 10).
Try to establish the following properties either by simulation or
verification:
1. If
the pending amount of money is sufficient (=5) and (only) the button
"requestCan" is pressed then a can will be given out.
2. A
can is only delivered if the pending amount of money is sufficient (=5)
3. As
soon as a can is delivered, the change is given to the cusotomer.
4. The
machine does not loose or produce money.
5. The
amount of pending coins in non-negative.
6. If
cash is pending and (only) the "cancel" button is pressed then the
machine will output all pending coins and no can.
Exercise 27
(Full Vending Machine)
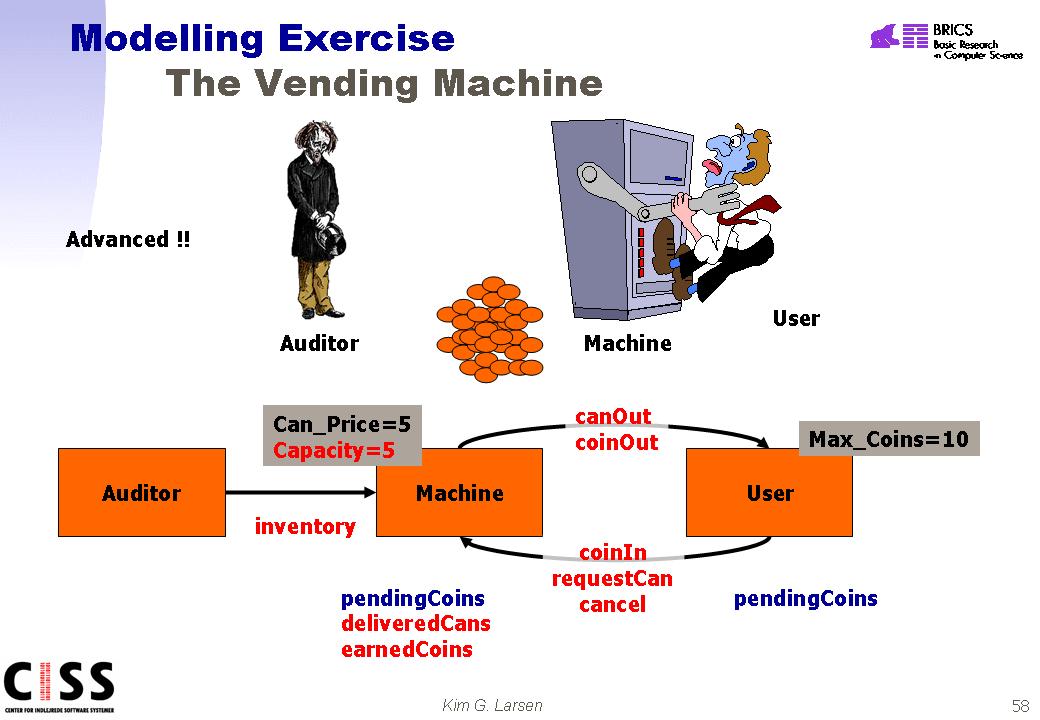 In this final
(and full) version of the vending machine the machine is supposed to have a
finite capacity (e.g. can only have 5 cans at any given moment). Also,
the machine should -- using local variables -- keep track of the number of cans
delivered and coins earned since last inventory. During inventory and
Auditor removes all earned coins (presumably taking them to a bank) and fill
the machine completely with cans (e.g. 5). Reconsider validations of the properties
of the previous exercise. In addition validate (by simulation or
verification) the additional properties:
In this final
(and full) version of the vending machine the machine is supposed to have a
finite capacity (e.g. can only have 5 cans at any given moment). Also,
the machine should -- using local variables -- keep track of the number of cans
delivered and coins earned since last inventory. During inventory and
Auditor removes all earned coins (presumably taking them to a bank) and fill
the machine completely with cans (e.g. 5). Reconsider validations of the properties
of the previous exercise. In addition validate (by simulation or
verification) the additional properties:
1. The
amount of earned coins is non-negative.
2. No
more than 5 cans can be delivered in a row without inventory.
3. After
delivering five cans without inventory, no more cash is accepted
4. Te
amount of earned/store coins is five times the number of delivered cans (since
the last inventory).