Exercises
- BRICK sorter
- Coffee machine
- Smart Light
- Protocol
- Veritication Options
- Over approximation
- Active clock reduction
- Test automata
- Data Link Protocol
- Theory
- The CSMA/CD Protocol
- Protocol
- The CSMA/CD Protocol continued
- Gossiping Girls
- Reduction
- Solving constraint systems
- Representation of regions
- Druzba
- Train-Gate Debugging
- Jug Filling
- Rush Hour
- Crossing the River
- How much can we loose?
- How much can we reach?
- A simple vending machine
- An extended vending machine
- The full vending machine.
- Tic Tac Toe with TIGA
- Chinese jugglers
Exercise 1 (BRICK sorter)
Experiment with the BRICK Sorter model (.xml) in UPPAAL. Experiment with the model of the
environment (including the number of bricks) to find out:
- under which circumstances the sorter operates correctly?, and
- under which circumstances the sorter misbehaves?
Use the functionalities of UPPAAL to explain what happens when the
sorter misbehaves.
Change the model of the controlling tasks in order to ensure
correct sorting of 2 bricks.
Exercise 2 (Coffee Machine)
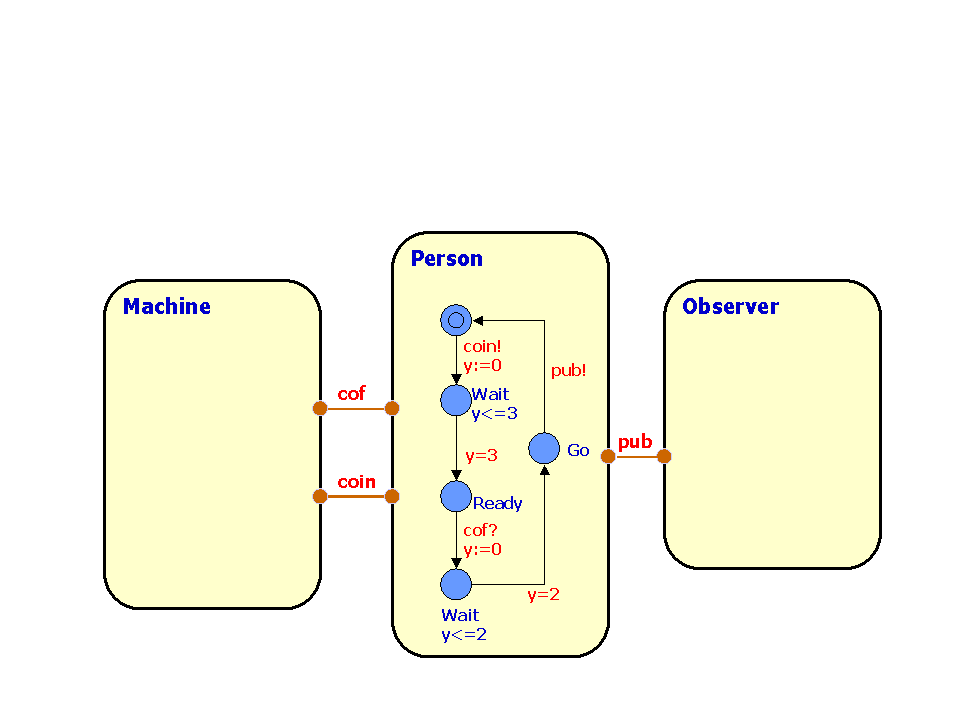
In this exercise you are asked to design the control of a
Machine (the control program) which will serve a coffee craving
Person (the environment). As you can see above the person
repeatedly (tries to) insert a coin, (tries to) extract coffee after
which (s)he will make a publication. Between each action the person
requires a suitable time-delay before being ready to participate in
the next one.
The machine takes some time for brewing the coffee and will
time-out if coffee has not been taken before a certain upper
time-limit.
As a requirement we want the overall behaviour to ensure that the
indicated Observer experiences a constant flow of publications
from the system. In particular we want the Observer to complain if at
any time more than 8 time-units elapses between two consecutive
publications. Model the Machine and Observer in UPPAAL and analyse the
behaviour of the system. Try to determine the maximum brewing
time allowed by the Machine in order that the above requirement is
met.
Exercise 3 (Smart Light)
Reconstruct a model of the Smart Light Switch (Intelligent Light
Control) taking timing into account. Below you see (from the
lecture) a timed automata model of the interface between the user
and the control program. Complete the model by designing appropriate
automata for the control program. Simulate the model and try to
estimate the minimum time to take the light to its maximum
intensity.

Exercise 4
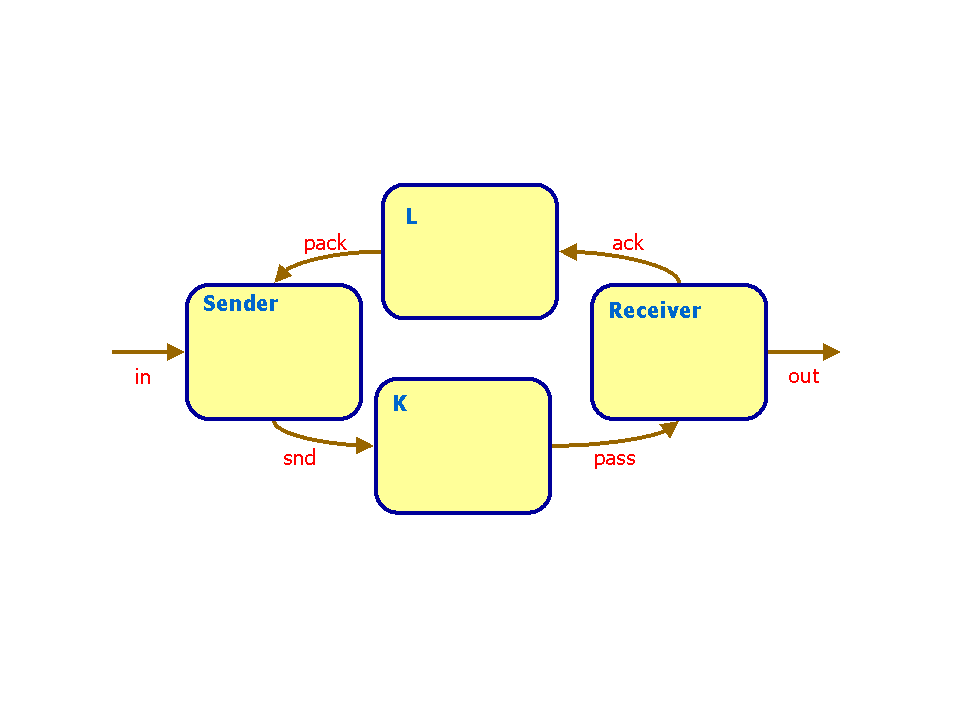
Consider the above system, where a SENDER and a RECEIVER wants to
communicate over a potential faulty communication line. In order
to allow the SENDER to detect when communication succeeds, two
(potentially faulty) communication media are used: one (K) for
transmitting the message from SENDER go RECEIVER and one (L) for
transmitting acknowledgements from the RECEIVER to the SENDER.
We assume that the both media are one-place buffers. Also, we
shall pay no attention to the actual message being
communicated.
Use UPPAAL to model and analyse communication systems of the above
type, where the media
The desired behaviour of the overall system is that of a one-place
buffer. Use UPPAAL to examine to what extent this behaviour is meet
in the various scenarios above.
Exercise 5 (Verification Options)
Experiment with the various verification options of UPPAAL on
Fischers Protocol(.xml, .q), The Soldiers Problem (.xml, .q) and the Gear
Box Controller (.xml, .q). Estimate the verification times
required and try to conclude on which options are to be prefered on
which examples.
Exercise 6 (Over-Approximations)
Construct an example where use of the verification option 'Over-approximation' gives the wrong answer.
Try to make your example as small as possible.
Exercise 7 (Active Clock Reduction)
Consider the timed automaton below:
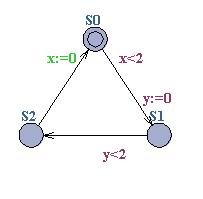
Calculate the active clocks for the three locations,
S0, S1 and S2. Compute the reachable symbolic
state-space of the timed automaton (using canonical DBM's for
representing constraint systems) first without any reduction and
afterwards with Active-clock
reduction. Compare the number of constraints and symbolic
states required to represent the reachable state-space in the two
cases.
Exercise 8 (Test automata)
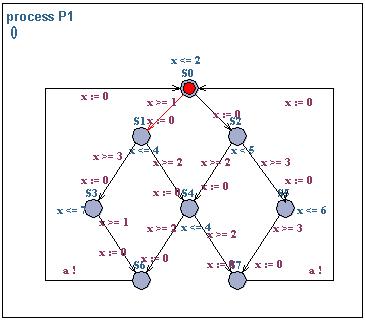
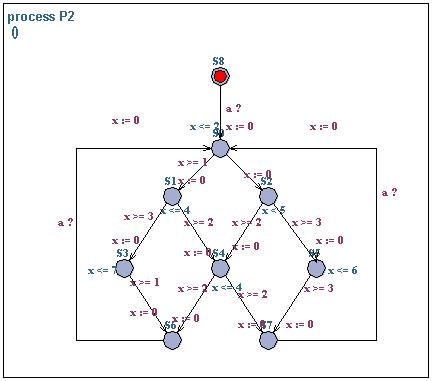
Consider the two timed automata P1 and P2 above. The
automata are interacting over an urgent channel a. Use the
testautomata or decoration technique for analysing bounded liveness
properties of the form:
- whenever P1.S1 then P2.S0 within t timeunits,
- whenever P1.S0 then P2.S4 within t timeunits,
- whenever P1.S0 then P2.S0 will not occur before t timeunits.
You can find downloadable version of the system here (.xml.
Exercise 9 (Modeling)
In this exercise you are to model, validate and verify a simple
data link protocol, where some unrealistic assumptions will be made in
order to keep the exercise simple.
The protocol specification is as follows: there are a
Sender, a Receiver and a Medium.
The medium can after reception of a message from the sender, do one
of two things: either the message is delivered to the receiver, or it
is lost. The loss of a message should be modeled by an internal
transition (unlabelled transition in UPPAAL), since the loss itself
does not constitute an observable event. When a message is lost a
time-out in the sender will occur - model this time-out as a
communication signal sent from the medium (in case of message loss) to
the sender. In case of a time-out, the sender will retransmit the
message. When the receiver gets a message an acknowledgment is sent to
the sender. Assume that the acknowledgment is sent
directly to the sender and not through any
medium.
Task 1: Model the above protocol in UPPAAL, and validate
using the simulator that it is functionally correct.
Redefine the protocol by modifying the receiver so that it reports
to the layer above when a message is receive. Add a test process (to
model the above layer) that receives the messages from the
receiver. Modify the sender to receive messages from the layer
above. Add another test process that generates messages to the sender
(modeling the above layer).
Task 2: Validate that the functionality of the refined
protocol is correct using the simulator.
Now modify the test environment so that the test sender increments
a shared integer variable i whenever a message is sent. Modify
the test receiver so that it decrements the variable i whenever
a message is received.
Task 3: Validate the protocol and verify that the value of
the variable i is always one or zero.
Task 4: What happens if the protocol is redefined in the
following way: acknowledgments are not sent at all from the receiver
to the sender? What happens if additionally the sender never expects
acknowledgments? Validate, verify and describe in words the behavior
of the resulting protocol.
Model the content of messages as (bounded) integer values
and change the models of the protocol and the test environment
consequently.
Task 5: Validate and afterwards verify, that the content of
a message when sent equals the content of the message when
received.
Exercise 10 (Theory)
JPK exercises 17, 18, 22.
Exercise 11 (Modeling, The CSMA/CD Protocol)
In this exercise you will study the Media Access Control (Mac) sub
layer of the Carrier Sense, Multiple Access with Control Detection
(CSMA/CD) communication protocol. The protocol specification consists
of two MAC entities, MAC1 and MAC2, interconnected by a
bi-directional medium M. The MAC entities are identical and can
both transmit and receive messages over the medium. This means that
collisions may occur on the medium (if the two MAC's transmit
simultaneously). It is assumed that collisions will be detected in
the medium and signaled to both MAC1 and MAC2.
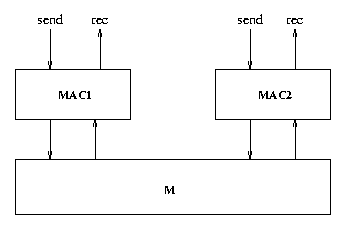
Overview of the MAC sub layer.
A model of the protocol is given in csma-cd-start.xml (the specification is
taken from "Verifying a CSMA/CD Protocol with CCS" by Joachim
Parrow. The specification uses the following synchronization actions
to describe the protocol events:
- send - service provided by Mac which reacts by transmitting a
message,
- rec - (receive) service provided by Mac, indicates that a
message is ready to be received,
- b - (begin) Mac begins message transmission to M,
- e - (end) Mac terminates message transmission to M,
- br - (begin receive) M begins message delivery to
Mac,
- er - (end receive) M terminates message delivery to
Mac,
- c - (collision) Mac is notified that a collision has
occurred on M.
Note that a message transmission is not modeled by a single
action. Instead the start of a transmission and the end of a
transmission are modeled by two separate actions (the actions b(r) and
e(r)). This is needed as there may be collisions detected in the
middle of a transmission. Note also that we use indexes on all actions
as there are two identical MAC entities.
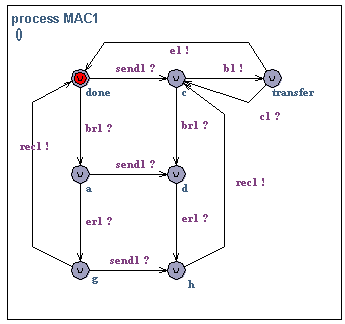
MAC1.
Initially, MAC1 accepts a service call (send1?). The MAC initiates
transmission (b1!), unless a message is in the process of being
received. If the transmission is successfully terminated (e1!) new
messages can be transmitted and the process is repeated. If a
collision occurs (c1?) the MAC attempts re-transmission of the
message. In all states (except when a message is being transmitted)
the MAC is willing to start receiving. A message may be received
(br1?) after which the MAC may not begin message transmission before
the end of message (er1?) has been received and the MAC has signaled
that the message is ready to be delivered (rec1!). However, the MAC
may receive a send request (send1?) if there is not already another
request waiting.
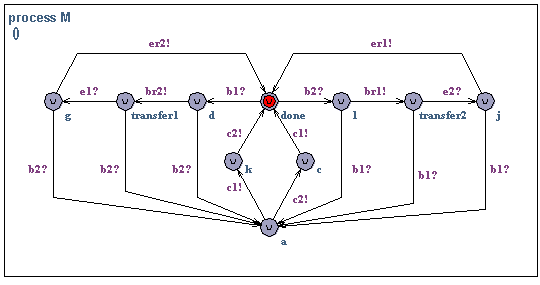
The medium M.
Initially, the medium accepts transmission from one of the MAC's
(b1? or b2?). We assume MAC1 (b1?) starts transmitting first (the case
for b2? is symmetric). The medium is assumed to be "half-duplex"
meaning that a full message must be transmitted (br2!, e1?, er2!)
before the next message can be accepted. If the receiving MAC
(i.e. MAC2) starts transmission (b2?) the medium interrupts the
transmission and signals collision (c1!, c2!) to both MAC1 and MAC1
(in any order).
Task 1: Open the protocol specification in csma-cd-start.xml and add a test
environment that "uses" the protocol. Validate that your system is
functionally correct using UPPAAL's simulator.
Task 2: Check (by verification) if the system is correct in
the sense that sent messages are received. How many messages can be
in transfer at the same time? Is it 1, 2 or more messages?
The model of the MAC is slightly inaccurate. In reality, a MAC
would be two processes: one sender performing the actions send!, b!,
e!, c? and one receiver performing the actions rec!, br? and er?
Task 3: Refine the protocol by letting each MAC consist of
two processes, a sender (S) and a receiver (R). The idea is to let S
perform all "horizontal" transitions and R all "vertical"
transitions. Replace MAC with S and R. Use UPPAAL to validate and
verify that the protocol no longer is correct.
Task 4: Redefine the protocol again so that it works, while
still keeping the S and R separate. This is a bit tricky. You may need
to add some synchronization channels (or data variables) to achieve
synchronization between S and R.
Exercise 12 (Modeling)
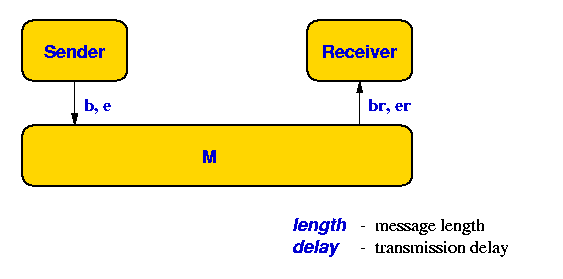
In this exercise you are asked to model a communication medium
M, a Sender, and a Receiver. The sender sends
messages of a fixed length length, which is the time
between the beginning and the end of a message. The medium has a
transmission delay delay, which is the time between the
beginning (or end) of a message is sent and the beginning (or end) of
a message is received. For example, if the beginning of a message is
sent at time t, it will be received by the receiver at time
t+delay.
Task 1: Model the system as a network of timed automata in
UPPAAL. Assume length<delay. Model the beginning and
end of each message. It is recommended to use integer constants in
UPPAAL for the values length and delay.
Task 2: Validate the sytem in the simulator and find out
what the total timed between "begin send" and "end
receive" is.
Task 3: Modify the medium M to handle messages of length
length>=delay.
Exercise 13 (Modeling: the CSMA/CD Protocol continued)
In this exercise we use the model of the CDMA/CD protocol. You are
asked to refine the model so that the sent messages have a fixed
length of time length, and to refine the communication
medium M to have a communication delay of time
delay..
Task 1: Model/modify the system with the assumption
length<delay.
Task 2: Verify that the system is correct in the sense that
all sent messages are indeed received..
Task 3: Refine the medium to allow messages of length
length>=delay.
Task 4: Verify that the refined system is correct in the
sense that all sent messages are indeed received.
Exercise 14 (Gossiping Girls)







Model and analyze the following gossiping girls problem in UPPAAL. A number
of girls initially know one distinct secret each. Each girl has access to a
phone which can be used to call another girl to share their secrets. Each time
two girls talk to each other they always exchange all secrets with each other (thus
after the phone call they both know all secrets they knew together before the
phone call). The girls can communicate only in pairs (no conference calls) but
it is possible that different pairs of girls talk concurrently.
Your tasks are as follows:
- Model the problem as a network of UPPAAL timed automata and use UPPAAL
to find the minimal number of phone calls needed for four girls to know all
secrets.
- Refine your model so that each phone call lasts exactly 60 seconds (for
simplicity this time duration is irrelevant of the number of exchanged
secrets). Find the minimum time needed to solve the gossiping girls problem
for four girls.
- Experiment with the UPPAAL search options breath-first and depth-first
search, upper and lower approximations, and with the diagnostic trace
settings fastest and shortest. Try to solve the problem for five girls.
- (For the keenest) Modify the model so that so that calls are
asynchronous (i.e. only the caller tells the receiver her secrets and not
vise versa).
Hint:
- Design a single template for all girls.
- For each girl, you may choose to remember the currently known secrets
either in a local array of booleans or using an integer variable (use a
binary encoding such that if a girl knows the secrets of e.g. girls 1 and 3
but does not know the secrets of girls 2 and 4, the value in the integer
variable will be (0101) binary = 5; you might find useful the operation |
for a bitwise OR).
Exercise 15 (Reduction)
This exercise will (hopefully) convince you that reachability
checking in the UPPAAL-model is a hard problem indeed (NP-hard); if
fact consider how you could use UPPAAL to analyse
satisfiability of propositional logic formulas, i.e. formulas
F build from propositional variables, b1, b2,
b3,...... using boolean connectives (and, or, negation,
....). You may assume that F is in conjunctive
normal form that is
F = C1 and C2 and C3 and ....... and
Cn, where
Ci = Li1 or
Li2 or Li3 or ......... or
Lik,
where
Lij is a variable bi
or a negated variable
~bi
Apply your idea for a construction to the formula:
(x or y
or ~z or u) and (~x or y or z or ~u) and ( x or ~y
or ~z) and (~x or y or ~u)
to see if the formula is satisfiable and if so to obtain a
satisfying assignment to the boolean variables x, y, z and
u.
Exercise 16 (Solving constraint systems)
The reachability algorithm of UPPAAL is based on efficient
representation and manipulation of Difference Constraints
Systems, i.e. linear equation systems between clock values where
each constraint is of the simple form (xj -
xj) <= bk.
In this exercise you should think about how to use UPPAAL to
decide whether a given difference constraint system has solutions or
not. Use your method to decide whether the following systems
have solutions or not. In case there are solutions try to use
UPPAAL to exhibit a single solution:
System 1: x1-x2<=1, x3-x1<=-1,
x1-x4<=3, x2-x3<=5.
System 2: x1-x2<=1, x1-x4<=-4,
x2-x3<=2, x2-x5<=7, x2-x6<=10, x4-x2<=2, x5-x1<=-1, x5-x4<=3,
x6-x3<=-8.
Consider also how to use UPPAAL to check for two difference
constraint systems D1 and D2 whether all solutions to D1 are also
solutions to D2. Use your 'method' to check whether the
constraint system 1 above is included in the following system 3:
System 3: x1-x3<=7, x3-x4<=2,
x3-x2<=4.
Exercise 18 (Druzba Mutex Problem)
Recall the Druzba mutex problem illustrated below.
.
The erroneous model
is given to you as well as the query-file.
Correct the model and supplement the query-file so that you obtain a
satisfactory system (and verifiable so).
Exercise 19 (Train-Gate Error
Correction)
The following contains an erroneous version
of the train-gate example. Here is the appropriate
query-file.
Use UPPAAL (simulation, verification) to pin-point and explain
the error(s). Having corrected the errors what is the minimum time one
can guarantee between a train requesting access to the crossing and actually
getting there?
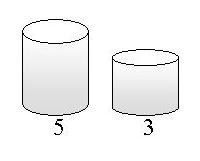
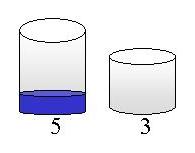
Exercise 20 (Jug Filling)
Consider the one-player Jug game illustrated below. In
this instance, two jugs are given with capacities 5 and 3 respectively.
Initially, the two jugs are empty. Now legal actions/rules on the jugs are
fill (we assume an infinite capacity tap by which we may fill any jug to the
rim), empty (we may at any time empty the complete content of a jug on
the floor), and pour the content of one jug into the other (of course
stopping the pouring if and when the rim is reached). Given this initial
configuration, and legal rules, we want to figure out whether it is possible to
reach a situation where the content of one jug is exactly 1. Make a
scalable model of the Jug game in UPPAAL (i.e. allowing for arbitrary numbers of
jugs with arbitrary capacity) and use it to find solutions bringing the above
instance into a final configuration where the large jug contains 2 units, 3
units, 4 units, and where the large jug contains 3 units and the small
jug contains 2 units.
Exercise 21 (Rush Hour)
In this exercise you are asked to model a solitair game and solve use UPPAAL
to solve the puzzle. The game is simple. You have a 6x6 board like shown on the
picture below. On the board you find a number of cars of different size (personal
vehicles and trucks). The goal of the game is to move the cars by driving
forward and backwards in such a way that the red car can leave the board at the
exit on the right side of the board. The cars cannot turn!


Task 1: Make a model of the game in UPPAAL.
Task 2: Use your model to solve the two puzzles shown in he second
picture. What is the shortest number of steps/moves needed to solve the
puzzle?
Task 3: Extend your model with timing constraint. Assume that it takes
a different amount of time to move the cars, e.g. 2 time units for the small
ones and 3 for the trucks (you can also choose to give each car its own time).
Try to experiment with different assumptions as to the number of hands/drivers,
i.e. how many cars can move at the same time.
Task 4: Use Uppaal to find the fastest way of solving the puzzle
(not measured in computation time, but in time it take to move all the cars).
Tip: Use Uppaals diagnostic trace feature and ask for the fastest trace.
For the keenest: you may want
to deal with the more challenging RAILROAD Rush Hour, which is on a 7x7 boards
and with 2x2 blockers that can move bort horizontal and vertical (see figure
below):

Exercise 22 (Crossing the River)
Help a familly to cross a river according to the following constraints:
- Max 2 persons on the boat,
- Mom not alone with boys,
- Dad ont alone with girls,
- Thief not alone with family,
- Only police officer, dad and mom can handle the boat.

Task 1: Make an Uppaal model of it and generate a feasible schedule.
Task 2: Add temporal constraints (e.g. each adult take a certain time
to cross the river with the boat) and try to find the quickest possible schedule.
Task 3: Try other parameters and constraints for this game. Determine
what is the feasibility limit depending on the number of boys, girls, prisonners.
Exercise 23 (How much can we loose)
Consider the following algorithm containing two parallel
processes both incrementing a common variable:
int n=0;
(n := n + 1 || n := n + 1)
In case the underlying computational model execute n:=n+1 as an
atomic operation the post condition is that n=2. But in case n:=n+1 is executed
as a number of atomic operations the post condition becomes 1 ≤ n ≤ 2.
Now we generalize the problem with respect to the number of
increments done by each processor. Consider the following algorithm in which
n:=n+1 is a non atomic operation, i.e. n:=n+1 is composed of the following
sequence of three atomic updates: r:=n; r:=r+1; n:=r
where r is a register local for the given parallel process:
const int k=…; int n=0;
Process P
do
n := n+1
k times
end P
( P || P )
For k=1, this program is equivalent to program 1.
Obviously (why?) the final value of n can not exceed 2*k. Intuition leads
us to believe that k is the smallest possible final value of n! However,
this intution is wrong. Use UPPAAL to model the above scenario (e.g. with
k=10) and use model-checking to find the smallest possible final value of n.
Try to increase the number of processes (e.g. consider ( P||P||P )).
Exercise 24 (How much can we reach)
Again we are considering the paralle execution of two, simple
(and identical) sequential programs:
const int n=1;
Process P
do
n := n+n
forever
( P || P )
Given that n:=n+n was atomic the possible values of n during
execution would be (all) powers of 2. However, consider the situation when
the update n:=n+n is carried out as the following sequence of three atomic
updates: r:=n; r:=r+n; n:=r. Now the question as to which values n
may achieve during execution is no longer obvious. Model the above
scenario in UPPAAL and try to figure out whether (and how) n can achieve the
values 2, 3, 8, 9, and 23. Which (and why) values can n achieve?
Exercise 25 (Simple Vending Machine)
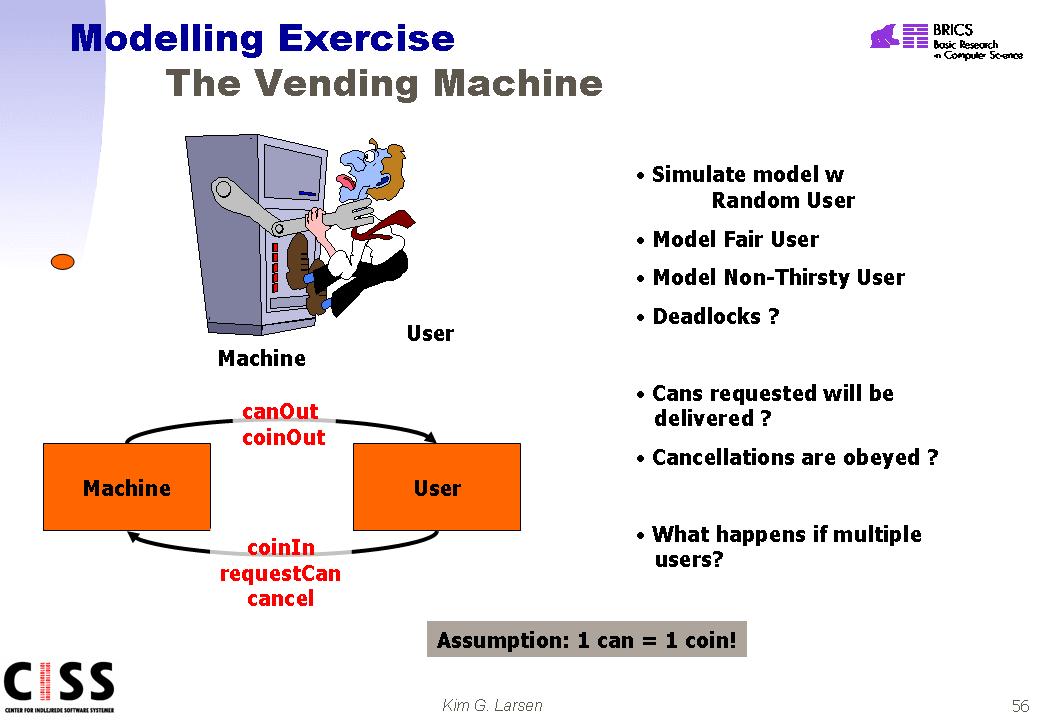 In
this exercise you are required to model a (very) simplified vending machine for
beverage cans. The vending machine is supposed to sell cans (containing
some interesting substance) to customers. In this simplest version, the
machine only sells a single kind of cans where a can cost one single unit (of
the currency of your choice). We also assume that the vending machine has
an unlimited number of available cans. Purchasing a can is usually
performed as follows:
In
this exercise you are required to model a (very) simplified vending machine for
beverage cans. The vending machine is supposed to sell cans (containing
some interesting substance) to customers. In this simplest version, the
machine only sells a single kind of cans where a can cost one single unit (of
the currency of your choice). We also assume that the vending machine has
an unlimited number of available cans. Purchasing a can is usually
performed as follows:
-
The customer inserts a coin into the machine
-
The customer may now either
- request a can, or
- cancel
-
Depending on the order of the customer the vending machine
should either provide a can or return the coin.
Model in UPPAAL the vending machine. Also make models of
various types of customers including a random customer (may at any given moment
non-deterministically try to insert a new coin, cancel an order, ...etc), a fair
customer (behaving as intended by the machine), a non-thirsty user (always
cancelling after insertion of coin). Validate the various configurations (machine
and a particular customer) by simulation. Check for (absence) of deadlock
in your model. Try to verify that cans reqeusted will be delivered, and
cancellations are objeyed. What happens if the configuration involves
multiple users (possibly of different type)?
Exercise 26 (Extended Vending Machine)
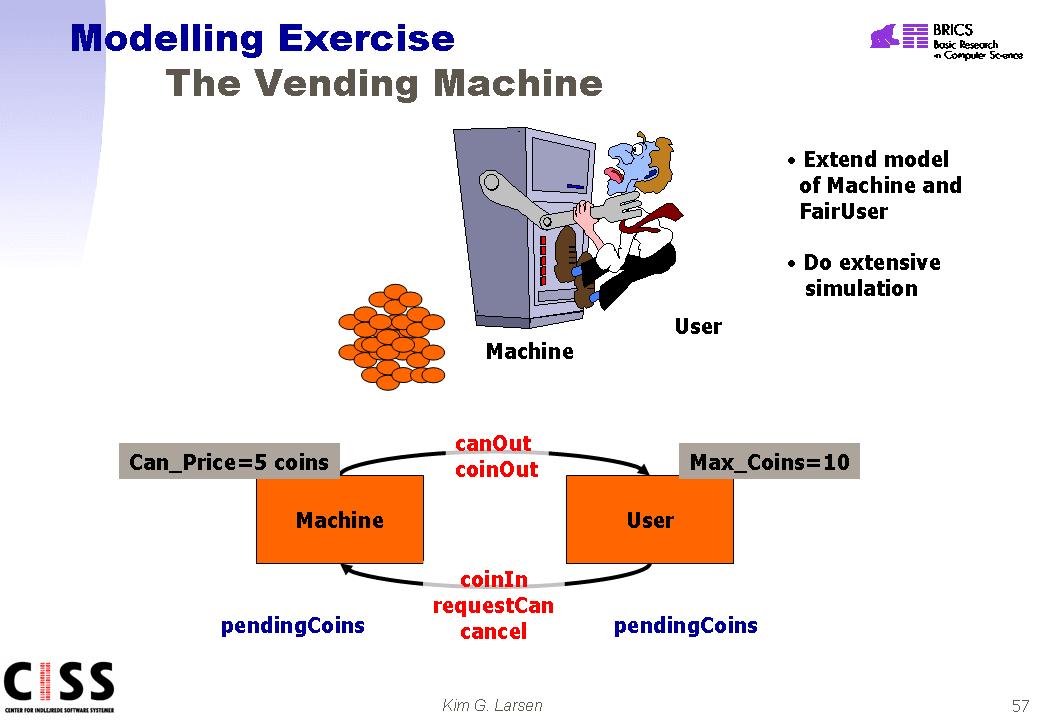 Extend
the model of the vending machine from the previous exercise so that the
price of a can is 5 units (or coins). Also change the behaviour of
the customers so that mulitple coins may be inserted before reqeusting a can is
attempted -- both the machine and the user should have their own local variable
(pendingCoins) for recording the credit of the customer. When a can is
requested the surplus of coins should be given back to the customer. To
make matters simpler you may assume that the user has a limited number of coins
(say 10).
Extend
the model of the vending machine from the previous exercise so that the
price of a can is 5 units (or coins). Also change the behaviour of
the customers so that mulitple coins may be inserted before reqeusting a can is
attempted -- both the machine and the user should have their own local variable
(pendingCoins) for recording the credit of the customer. When a can is
requested the surplus of coins should be given back to the customer. To
make matters simpler you may assume that the user has a limited number of coins
(say 10).
Try to establish the following properties either by simulation
or verification:
-
If the pending amount of money is sufficient (=5) and (only)
the button "requestCan" is pressed then a can will be given out.
-
A can is only delivered if the pending amount of money is
sufficient (=5)
-
As soon as a can is delivered, the change is given to the
cusotomer.
-
The machine does not loose or produce money.
-
The amount of pending coins in non-negative.
-
If cash is pending and (only) the "cancel" button is pressed
then the machine will output all pending coins and no can.
Exercise 27 (Full Vending Machine)
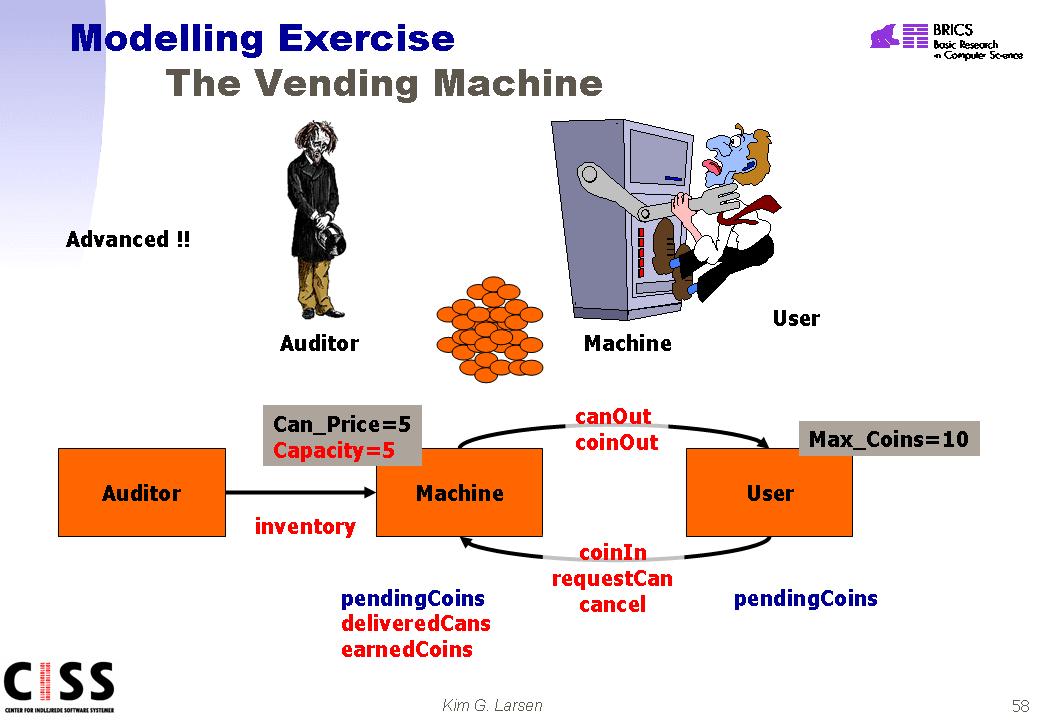 In
this final (and full) version of the vending machine the machine is supposed to
have a finite capacity (e.g. can only have 5 cans at any given moment).
Also, the machine should -- using local variables -- keep track of the number of
cans delivered and coins earned since last inventory. During inventory and
Auditor removes all earned coins (presumably taking them to a bank) and fill the
machine completely with cans (e.g. 5). Reconsider validations of the
properties of the previous exercise. In addition validate (by simulation
or verification) the additional properties:
In
this final (and full) version of the vending machine the machine is supposed to
have a finite capacity (e.g. can only have 5 cans at any given moment).
Also, the machine should -- using local variables -- keep track of the number of
cans delivered and coins earned since last inventory. During inventory and
Auditor removes all earned coins (presumably taking them to a bank) and fill the
machine completely with cans (e.g. 5). Reconsider validations of the
properties of the previous exercise. In addition validate (by simulation
or verification) the additional properties:
-
The amount of earned coins is non-negative.
-
No more than 5 cans can be delivered in a row without
inventory.
-
After delivering five cans without inventory, no more cash
is accepted
-
Te amount of earned/store coins is five times the number of
delivered cans (since the last inventory).
Model this classic game with UPPAAL-TIGA and check that
there is no guaranteed way to always win.
Model a (Chinese) performer who needs to spin plates that are on a stick to
prevent them from falling. The juggler can spin a plate quickly to get some
time, in which case the plate is stable for a short time, or he can spin
it a while longer and the plate is stable longer as well. Unfortunately,
no one knows (because of a flying mosquito) when a stable plate
becomes unstable (after some minimal amount of time of course). Plates crash
after a while if they are not spun. Use up to 3 plates in your model with
different timing values for the plates (for small or big plates). Find out
the strategy to keep the plates from falling.

















 Extend
the model of the vending machine from the previous exercise so that the
price of a can is 5 units (or coins). Also change the behaviour of
the customers so that mulitple coins may be inserted before reqeusting a can is
attempted -- both the machine and the user should have their own local variable
(pendingCoins) for recording the credit of the customer. When a can is
requested the surplus of coins should be given back to the customer. To
make matters simpler you may assume that the user has a limited number of coins
(say 10).
Extend
the model of the vending machine from the previous exercise so that the
price of a can is 5 units (or coins). Also change the behaviour of
the customers so that mulitple coins may be inserted before reqeusting a can is
attempted -- both the machine and the user should have their own local variable
(pendingCoins) for recording the credit of the customer. When a can is
requested the surplus of coins should be given back to the customer. To
make matters simpler you may assume that the user has a limited number of coins
(say 10).  In
this final (and full) version of the vending machine the machine is supposed to
have a finite capacity (e.g. can only have 5 cans at any given moment).
Also, the machine should -- using local variables -- keep track of the number of
cans delivered and coins earned since last inventory. During inventory and
Auditor removes all earned coins (presumably taking them to a bank) and fill the
machine completely with cans (e.g. 5). Reconsider validations of the
properties of the previous exercise. In addition validate (by simulation
or verification) the additional properties:
In
this final (and full) version of the vending machine the machine is supposed to
have a finite capacity (e.g. can only have 5 cans at any given moment).
Also, the machine should -- using local variables -- keep track of the number of
cans delivered and coins earned since last inventory. During inventory and
Auditor removes all earned coins (presumably taking them to a bank) and fill the
machine completely with cans (e.g. 5). Reconsider validations of the
properties of the previous exercise. In addition validate (by simulation
or verification) the additional properties: